题目内容
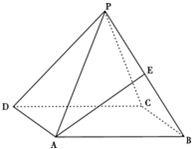 如图,正四棱锥P-ABCD中,侧棱PA与底面ABCD所成角的正切值为
如图,正四棱锥P-ABCD中,侧棱PA与底面ABCD所成角的正切值为
| ||
| 2 |
(1)求侧面PAD与底面ABCD所成二面角的大小;
(2)若E是PB中点,求异面直线PD与AE所成角的正切值.
分析:(1)连接AC、BD交于点O,连接PO,则PO⊥面ABCD,则∠PAO就是PA与底面ABCD所成的角,设AB=1,则可得则PO=AO•tan∠PAO
设F为AD中点,连FO、PF,易知OF⊥AD,PF⊥AD,所以∠PFO就是侧面PAD与底面ABCD所成二面角的平面角,在Rt△POF中可求∠PFO
(2)容易证明EO
PD.可得∠AEO就是异面直线PD与AE所成的角,在Rt△AOE中求解
设F为AD中点,连FO、PF,易知OF⊥AD,PF⊥AD,所以∠PFO就是侧面PAD与底面ABCD所成二面角的平面角,在Rt△POF中可求∠PFO
(2)容易证明EO
| ∥ |
. |
| 1 |
| 2 |
解答: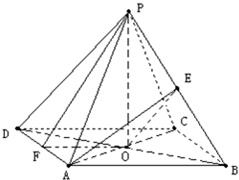 解:(1)连接AC、BD交于点O,连接PO,则PO⊥面ABCD,(1分)
解:(1)连接AC、BD交于点O,连接PO,则PO⊥面ABCD,(1分)
∴∠PAO就是PA与底面ABCD所成的角,∴tan∠PAO=
.(2分)
设AB=1,则PO=AO•tan∠PAO=
×
=
.(3分)
设F为AD中点,连FO、PF,
易知OF⊥AD,PF⊥AD,所以∠PFO就是侧面PAD与底面ABCD所成二面角的平面角.(4分)
在Rt△POF中,tan∠PFO=
=
/
=
,
∴∠PFO=60°,即侧面PAD与底面ABCD所成二面角的大小为60°;(5分)
(2)连接EO,由于O为BD中点,E为PB中点,所以,EO
PD.
∴∠AEO就是异面直线PD与AE所成的角.(6分)
在Rt△POD中,PD=
=
.∴EO=
.(7分)
由AO⊥BD,AO⊥PO可知AO⊥面PBD.所以,AO⊥EO(8分)
在Rt△AOE中,tan∠AEO=
=
/
=
,
即异面直线PD与AE所成角的正切值为
.(9分)
 解:(1)连接AC、BD交于点O,连接PO,则PO⊥面ABCD,(1分)
解:(1)连接AC、BD交于点O,连接PO,则PO⊥面ABCD,(1分)∴∠PAO就是PA与底面ABCD所成的角,∴tan∠PAO=
| ||
| 2 |
设AB=1,则PO=AO•tan∠PAO=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
设F为AD中点,连FO、PF,
易知OF⊥AD,PF⊥AD,所以∠PFO就是侧面PAD与底面ABCD所成二面角的平面角.(4分)
在Rt△POF中,tan∠PFO=
| PO |
| FO |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
∴∠PFO=60°,即侧面PAD与底面ABCD所成二面角的大小为60°;(5分)
(2)连接EO,由于O为BD中点,E为PB中点,所以,EO
| ∥ |
. |
| 1 |
| 2 |
∴∠AEO就是异面直线PD与AE所成的角.(6分)
在Rt△POD中,PD=
| OD2+PO2 |
| ||
| 2 |
| ||
| 4 |
由AO⊥BD,AO⊥PO可知AO⊥面PBD.所以,AO⊥EO(8分)
在Rt△AOE中,tan∠AEO=
| AO |
| EO |
| ||
| 2 |
| ||
| 4 |
2
| ||
| 5 |
即异面直线PD与AE所成角的正切值为
2
| ||
| 5 |
点评:本题主要考查了直线与平面所成角及二面角的平面角的求解,解决问题(1)的关键是要找到与已知平面垂直的直线,从而把线面角转化为线线角,还要注意线面角的范围:[0,
];解决问题(2)的关键是要寻求与已知异面直线平行的直线,从而把异面直线所成的角转化为相交直线所成的角,其范围:(0,
)
| π |
| 2 |
| π |
| ,2 |

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
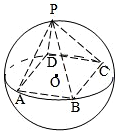 如图,正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上,点P在球面上,若
如图,正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上,点P在球面上,若 如图,正四棱锥P-ABCD的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )
如图,正四棱锥P-ABCD的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( ) (2008•上海一模)如图,正四棱锥P-ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,且已知
(2008•上海一模)如图,正四棱锥P-ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,且已知 如图,正四棱锥P-ABCD中,PA=2,AB=1,M是侧棱PC的中点,O为底面正方形的中心.
如图,正四棱锥P-ABCD中,PA=2,AB=1,M是侧棱PC的中点,O为底面正方形的中心. (2009•温州一模)如图是正四棱锥P-ABCD的三视图,其中正视图是边长为1的正三角形,则这个四棱锥的表面积是( )
(2009•温州一模)如图是正四棱锥P-ABCD的三视图,其中正视图是边长为1的正三角形,则这个四棱锥的表面积是( )