题目内容
 如图,正四棱锥P-ABCD中,PA=2,AB=1,M是侧棱PC的中点,O为底面正方形的中心.
如图,正四棱锥P-ABCD中,PA=2,AB=1,M是侧棱PC的中点,O为底面正方形的中心.(1)求证:PA∥平面BDM;
(2)求二面角P-BC-A的余弦值.
分析:(1)连接MO,通过M是正四棱锥P-ABCD侧棱PC的中点,O为底面正方形的中心,证明MO∥PA,然后证明PA∥平面BDM;
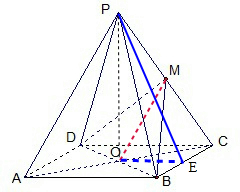
(2)取BC的中点E,连接PE,OE,说明二面角P-BC-A的平面角是∠PEO,利用题目条件,即可解三角形求出二面角P-BC-A的余弦值.
(2)取BC的中点E,连接PE,OE,说明二面角P-BC-A的平面角是∠PEO,利用题目条件,即可解三角形求出二面角P-BC-A的余弦值.
解答: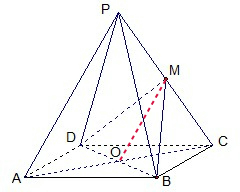 解:(1)证明:连接MO,因为几何体是正四棱锥P-ABCD,M是侧棱PC的中点,O为底面正方形的中心.
解:(1)证明:连接MO,因为几何体是正四棱锥P-ABCD,M是侧棱PC的中点,O为底面正方形的中心.
所以MO∥PA,MO?平面BDM,PA?平面BDM,
∴PA∥平面BDM;
(2)取BC的中点E,连接PE,OE,因为几何体是正四棱锥P-ABCD,O为底面正方形的中心,
∴PE⊥BC,OE⊥BC,∴二面角P-BC-A的平面角是∠PEO,
∵PA=2,AB=1,∴OE=
,PE=
=
,
cos∠PEO=
=
=
.
二面角P-BC-A的余弦值为:
.
 解:(1)证明:连接MO,因为几何体是正四棱锥P-ABCD,M是侧棱PC的中点,O为底面正方形的中心.
解:(1)证明:连接MO,因为几何体是正四棱锥P-ABCD,M是侧棱PC的中点,O为底面正方形的中心.所以MO∥PA,MO?平面BDM,PA?平面BDM,
∴PA∥平面BDM;
(2)取BC的中点E,连接PE,OE,因为几何体是正四棱锥P-ABCD,O为底面正方形的中心,
∴PE⊥BC,OE⊥BC,∴二面角P-BC-A的平面角是∠PEO,
∵PA=2,AB=1,∴OE=
| 1 |
| 2 |
22-(
|
| ||
| 2 |
cos∠PEO=
| OE |
| PE |
| ||||
|
| ||
| 15 |
二面角P-BC-A的余弦值为:
| ||
| 15 |

点评:本题考查直线与平面的平行,二面角的求法,考查空间想象能力,作图能力以及计算能力,解题的关键是正确利用直线与平面平行的判定定理,准确找出二面角的平面角.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
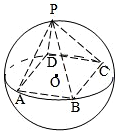 如图,正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上,点P在球面上,若
如图,正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上,点P在球面上,若 如图,正四棱锥P-ABCD的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )
如图,正四棱锥P-ABCD的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( ) (2008•上海一模)如图,正四棱锥P-ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,且已知
(2008•上海一模)如图,正四棱锥P-ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,且已知 (2009•温州一模)如图是正四棱锥P-ABCD的三视图,其中正视图是边长为1的正三角形,则这个四棱锥的表面积是( )
(2009•温州一模)如图是正四棱锥P-ABCD的三视图,其中正视图是边长为1的正三角形,则这个四棱锥的表面积是( )