题目内容
14.已知$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(2,1),(1)当k为何值时,k$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$垂直?
(2)若$\overrightarrow{AB}$=2$\overrightarrow{a}$+3$\overrightarrow{b}$,$\overrightarrow{BC}$=$\overrightarrow{a}$+m$\overrightarrow{b}$且A、B、C三点共线,求m的值.
分析 (1)由已知向量的坐标求出k$\overrightarrow{a}$-$\overrightarrow{b}$的坐标,再由k$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$垂直,结合向量垂直的坐标运算得答案;
(2)求出$\overrightarrow{AB}$,$\overrightarrow{BC}$的坐标,由向量共线的坐标运算列式求得m值.
解答 解:(1)∵$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(2,1),
∴k$\overrightarrow{a}$-$\overrightarrow{b}$=(k-2,-1),
又k$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$垂直,得2(k-2)-1=0,即k=$\frac{5}{2}$;
(2)$\overrightarrow{AB}$=2$\overrightarrow{a}$+3$\overrightarrow{b}$=(8,3),$\overrightarrow{BC}$=$\overrightarrow{a}$+m$\overrightarrow{b}$=(1+2m,m),
∵A、B、C三点共线,∴$\overrightarrow{AB}∥\overrightarrow{BC}$,
则8m-3(1+2m)=0,解得:m=$\frac{3}{2}$.
点评 本题考查平面向量的数量积运算,考查了向量共线、垂直的坐标运算,是中档题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
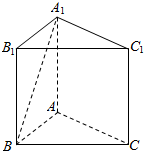 如图,在正三棱柱ABC-A1B1C1中,底面边长为2,异面直线A1B与B1C1所成角的大小为$arccos\frac{{\sqrt{5}}}{10}$.
如图,在正三棱柱ABC-A1B1C1中,底面边长为2,异面直线A1B与B1C1所成角的大小为$arccos\frac{{\sqrt{5}}}{10}$.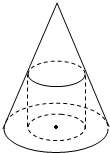 已知:如图所示,一个圆锥的底面半径为30,高为40,在其中有一个高为20的内接圆柱.
已知:如图所示,一个圆锥的底面半径为30,高为40,在其中有一个高为20的内接圆柱.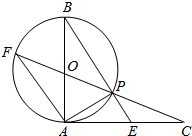 如图所示,AB是⊙O的直径,AC切⊙O于点A,AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E.
如图所示,AB是⊙O的直径,AC切⊙O于点A,AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E.