题目内容
9.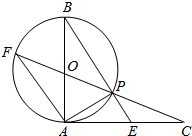 如图所示,AB是⊙O的直径,AC切⊙O于点A,AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E.
如图所示,AB是⊙O的直径,AC切⊙O于点A,AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E.(1)求证:$\frac{AP}{PC}$=$\frac{FA}{AB}$;
(2)若⊙O的直径AB=1,求tan∠CPE的值.
分析 (1)由弦切角定理,可得∠PAC=∠F,进而可得△APC∽△FAC,结合AC=AB,和相似三角形对应边成比例,可证得:$\frac{AP}{PC}$=$\frac{FA}{AB}$.
(2)若⊙O的直径AB=1,由切割线定理可得PC=$\frac{\sqrt{5}-1}{2}$,进而根据FA∥BE,即∠CPE=∠F,解Rt△FAP可得答案.
解答 证明:(1)∵AC切⊙O于点A,PA是弦,
∴∠PAC=∠F,
∵∠C=∠C,
∴△APC∽△FAC,
∴$\frac{AP}{FA}=\frac{PC}{AC}$,
∵AC=AB,
∴$\frac{AP}{PC}$=$\frac{FA}{AB}$.
解:(2)∵AC切⊙O于点A,CPF为⊙O的割线,
则有AC2=CP•CF=CP(CP+PF),
∵PF=AC=AB=1,
∴PC=$\frac{\sqrt{5}-1}{2}$.
∵FA∥BE,
∴∠CPE=∠F,
∵FP为⊙O的直径,
∴∠FAP=90°,
由(1)中证得$\frac{AP}{FA}=\frac{PC}{AC}$,
在Rt△FAP中,tan∠F=$\frac{\sqrt{5}-1}{2}$.
∴tan∠CPE=$\frac{\sqrt{5}-1}{2}$.
点评 本题考查的知识点弦切角定理,圆周角定理,相似三角形的判定与性质,切割线定理,难度中档.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.若函数f(x)=x2+2(a-1)x在区间[4,+∞)上是增函数,则实数a的取值范围是( )
| A. | a≥-3 | B. | a≤-3 | C. | a≤3 | D. | a≤5 |
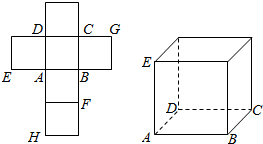 一个正方体的平面展开图及该正方体的直观图的示意图如图所示.
一个正方体的平面展开图及该正方体的直观图的示意图如图所示. 如图,在直三棱柱ABC-A1B1C1中,AB=BC=AC=2,AA1=3,点M是B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=AC=2,AA1=3,点M是B1C1的中点.