题目内容
5.在△ABC中,角A,B,C的对边分别为a、b、c,tanC=$\frac{sinA+sinB}{cosA+cosB}$.(1)求角C的大小;
(2)若△ABC的外接圆直径为1,求△ABC面积S的取值范围.
分析 (1)先将tanC写成$\frac{sinC}{cosC}$,再展开化为sin(C-A)=sin(B-C),从而求得A+B;
(2)先用正弦定理,再用面积公式,结合A-B的范围,求面积的范围.
解答 解:(1)∵tanC=$\frac{sinA+sinB}{cosA+cosB}$,∴$\frac{sinC}{cosC}$=$\frac{sinA+sinB}{cosA+cosB}$,
即sinCcosA+sinCcosB=cosCsinA+cosCsinB,
所以,sinCcosA-cosCsinA=cosCsinB-sinCcosB,
因此,sin(C-A)=sin(B-C),
所以,C-A=B-C或C-A=π-(B-C)(不成立),
即2C=A+B,故C=$\frac{π}{3}$;
(2)根据正弦定理,外接圆直径2R=$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=1,
所以,a=2RsinA=sinA,b=2RsinB=sinB,
而S△ABC=$\frac{1}{2}$absinC=$\frac{\sqrt{3}}{4}$sinAsinB
=$\frac{\sqrt{3}}{8}$[cos(A-B)-cos(A+B)]
=$\frac{\sqrt{3}}{8}$[cos(A-B)+$\frac{1}{2}$],
其中,A+B=$\frac{2π}{3}$,所以,A-B∈(-$\frac{2π}{3}$,$\frac{2π}{3}$),
因此,cos(A-B)∈(-$\frac{1}{2}$,1],
所以,S△ABC=∈(0,$\frac{3\sqrt{3}}{16}$],
故△ABC面积S的取值范围为:$S∈({0,\frac{3}{16}\sqrt{3}}]$.
点评 本题主要考查了三角函数的恒等变换,涉及同角三角函数基本关系式,两角和差的正弦公式,以及运用正弦定理解三角形和面积的求解,属于中档题.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案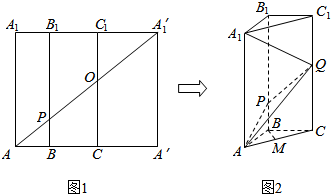 如图1所示:在边长为12的正方形AA′A${\;}_{1}^{′}$A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA${\;}_{1}^{′}$分别交BB1、CC1于P,Q两点,将正方形沿BB1、CC1折叠,使得A′A${\;}_{1}^{′}$与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.
如图1所示:在边长为12的正方形AA′A${\;}_{1}^{′}$A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA${\;}_{1}^{′}$分别交BB1、CC1于P,Q两点,将正方形沿BB1、CC1折叠,使得A′A${\;}_{1}^{′}$与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.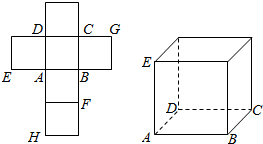 一个正方体的平面展开图及该正方体的直观图的示意图如图所示.
一个正方体的平面展开图及该正方体的直观图的示意图如图所示. 如图,在直三棱柱ABC-A1B1C1中,AB=BC=AC=2,AA1=3,点M是B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=AC=2,AA1=3,点M是B1C1的中点.