题目内容
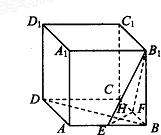 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为棱AB和BC的中点,EF交BD于H.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为棱AB和BC的中点,EF交BD于H.(1)求二面角B1-EF-B的正切值;
(2)试在棱B1B上找一点M,使D1M⊥平面EFB1,并证明你的结论;
(3)求点D1到平面EFB1的距离.
分析:(1)连AC、B1H,根据二面角平面角的定义可知∠B1HB为二面角B1-EF-B的平面角,在Rt△B1HB中求出此角的正切值即可;
(2)在棱B1B上取中点M,连D1M、C1M,欲证D1M⊥平面EFB1,根据直线与平面垂直的判定定理可知只需证D1M与平面EFB1内两相交直线垂直,而EF⊥D1M,B1F⊥D1M,满足定理条件;
(3)设D1M与平面EFB1交于点N,则D1N为点D1到平面EFB1的距离,在Rt△MB1D1中利用射影定理求出D1N即可.
(2)在棱B1B上取中点M,连D1M、C1M,欲证D1M⊥平面EFB1,根据直线与平面垂直的判定定理可知只需证D1M与平面EFB1内两相交直线垂直,而EF⊥D1M,B1F⊥D1M,满足定理条件;
(3)设D1M与平面EFB1交于点N,则D1N为点D1到平面EFB1的距离,在Rt△MB1D1中利用射影定理求出D1N即可.
解答:解:(1)连AC、B1H,则EF∥AC,
∵AC⊥BD,所以BD⊥EF.
∵B1B⊥平面ABCD,所以B1H⊥EF,
∴∠B1HB为二面角B1-EF-B的平面角.(2分)
在Rt△B1BH中,B1B=a,BH=
a.
∴tan∠B1HB=
=2
故二面角B1-EF-B的正切值为2
(4分)
(2)在棱B1B上取中点M,连D1M、C1M.
∵EF⊥平面B1BDD1,
所以EF⊥D1M.(6分)
在正方形BB1C1C中,因为M、F分别为BB1、BC的中点,
∴B1F⊥C1M(8分)
又因为D1C1⊥平面BCC1B1,所以B1F⊥D1C1,
所以B1F⊥D1M,
∴D1M⊥平面EFB1(10分)
(3)设D1M与平面EFB1交于点N,则D1N为点D1到平面EFB1的距离.(11分)
在Rt△MB1D1中,D1B12=D1N•D1M(12分)
∵D1B1=
a,D1M=
a,
所以D1N=
=
a,
故点D1到平面EFB1的距离为
a.(14分)
∵AC⊥BD,所以BD⊥EF.
∵B1B⊥平面ABCD,所以B1H⊥EF,
∴∠B1HB为二面角B1-EF-B的平面角.(2分)
在Rt△B1BH中,B1B=a,BH=
| ||
| 4 |
∴tan∠B1HB=
| B1B |
| BH |
| 2 |
故二面角B1-EF-B的正切值为2
| 2 |

(2)在棱B1B上取中点M,连D1M、C1M.
∵EF⊥平面B1BDD1,
所以EF⊥D1M.(6分)
在正方形BB1C1C中,因为M、F分别为BB1、BC的中点,
∴B1F⊥C1M(8分)
又因为D1C1⊥平面BCC1B1,所以B1F⊥D1C1,
所以B1F⊥D1M,
∴D1M⊥平面EFB1(10分)
(3)设D1M与平面EFB1交于点N,则D1N为点D1到平面EFB1的距离.(11分)
在Rt△MB1D1中,D1B12=D1N•D1M(12分)
∵D1B1=
| 2 |
| 3 |
| 2 |
所以D1N=
D1
| ||
| D1M |
| 4 |
| 3 |
故点D1到平面EFB1的距离为
| 4 |
| 3 |
点评:本题主要考查了二面角及其度量,以及点、线、面间的距离计算和直线与平面垂直的判定,考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )
如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( ) ,当
,当 取什么位置时,三棱柱的体积最大?
取什么位置时,三棱柱的体积最大?





