题目内容
设函数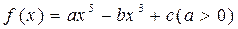 .
.
(1)若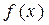 在
在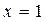 和
和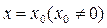 处有不同的极值,且极大值为4,
处有不同的极值,且极大值为4,
极小值为1,求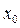 及实数
及实数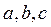 的值;
的值;
(2) 若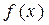 在
在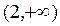 上单调递增且
上单调递增且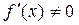 ,求
,求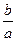 的最大值.
的最大值.
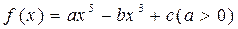 .
. (1)若
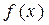 在
在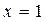 和
和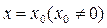 处有不同的极值,且极大值为4,
处有不同的极值,且极大值为4,极小值为1,求
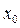 及实数
及实数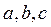 的值;
的值;(2) 若
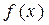 在
在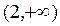 上单调递增且
上单调递增且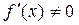 ,求
,求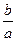 的最大值.
的最大值. 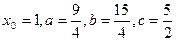 ,
,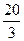
解:(1)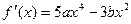 ,依题意得:
,依题意得:
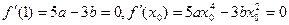
又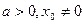 ,则
,则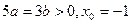 ,
,
所以当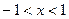 时,
时,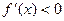 ;当
;当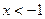 或
或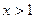 时,
时,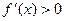 ,
,
故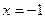 时函数有极大值,
时函数有极大值,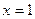 时函数有极小值;
时函数有极小值;
则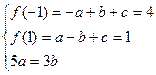 得
得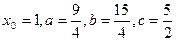
(2)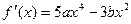 ,因为
,因为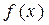 在
在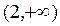 上单调递增,且
上单调递增,且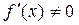 ,所以
,所以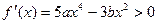 在
在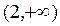 上恒成立。
上恒成立。
即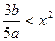 在
在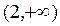 上恒成立,所以
上恒成立,所以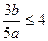 ,即
,即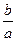 的最大值为
的最大值为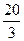
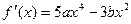 ,依题意得:
,依题意得: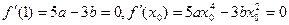
又
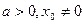 ,则
,则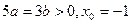 ,
,所以当
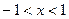 时,
时,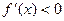 ;当
;当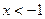 或
或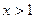 时,
时,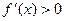 ,
,故
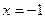 时函数有极大值,
时函数有极大值,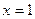 时函数有极小值;
时函数有极小值;则
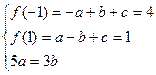 得
得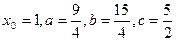
(2)
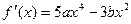 ,因为
,因为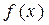 在
在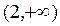 上单调递增,且
上单调递增,且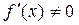 ,所以
,所以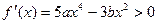 在
在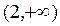 上恒成立。
上恒成立。即
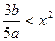 在
在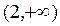 上恒成立,所以
上恒成立,所以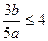 ,即
,即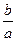 的最大值为
的最大值为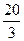

练习册系列答案
相关题目
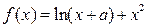
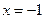 时,
时,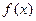 取得极值,求
取得极值,求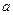 的值,并讨论
的值,并讨论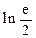 .
.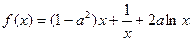 .
.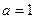 时,求
时,求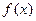 的最小值;
的最小值; 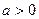 时,求
时,求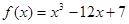 在
在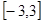 上的最大值与最小值的差是
上的最大值与最小值的差是



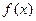 =
=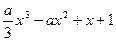 .
.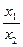 ≤5,求a的取值范围。12分
≤5,求a的取值范围。12分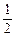
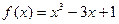 在闭区间
在闭区间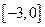 上的最大值,最小值分别是( )
上的最大值,最小值分别是( )
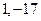
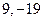

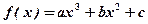 ,其导函数图象如图1所示,
,其导函数图象如图1所示,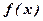 的极小值是 ( * )
的极小值是 ( * ) 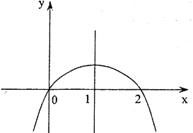


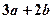
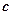
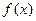 的定义域为区间
的定义域为区间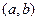 ,导函数
,导函数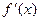 在
在
 个
个 个
个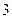 个
个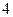 个[
个[