题目内容
16.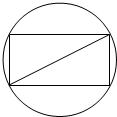 如图,把截面半径为10cm的圆形木头锯成矩形木料,如果矩形一边长为x,面积为y,试将y表表示成x的函数,并画出函数的大致图象,并判断怎样锯才能使得截面面积最大?
如图,把截面半径为10cm的圆形木头锯成矩形木料,如果矩形一边长为x,面积为y,试将y表表示成x的函数,并画出函数的大致图象,并判断怎样锯才能使得截面面积最大?
分析 首先根据矩形的一边长为xcm,表示出另外一边的长度,然后直接列出y关于x的函数.
解答 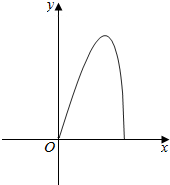 解:∵矩形的一边长为xcm,
解:∵矩形的一边长为xcm,
∴矩形的另一边长为$\sqrt{100-{x}^{2}}$cm,
∴y=x•$\sqrt{100-{x}^{2}}$,则对应的图象为:
∵直径为20cm,
∴0<x<10,
∴y=x•$\sqrt{100-{x}^{2}}$≤$\frac{{x}^{2}+100-{x}^{2}}{2}$=50,当且仅当x=$\sqrt{100-{x}^{2}}$,
即x=$\sqrt{50}$=5$\sqrt{2}$时,面积最大,最大值为50.
点评 本题考查函数模型的选择与应用,通过对实际问题的分析,抽象出数学模型,把y表示为x的函数,属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
11.把32(4)化为二进制数为( )
| A. | 1100(2) | B. | 1011(2) | C. | 110(2) | D. | 1110(2) |
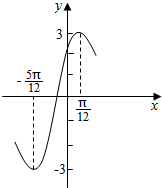 如图,是函数y=Asin(ωx+φ)+k(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
如图,是函数y=Asin(ωx+φ)+k(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.