题目内容
1.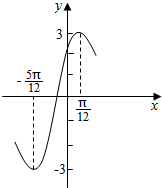 如图,是函数y=Asin(ωx+φ)+k(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
如图,是函数y=Asin(ωx+φ)+k(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.(1)试求此函数的解析式.
(2)求f(x)的单调递增区间;
(3)求函数f(x)图象的对称轴的方程和对称中心的坐标.
分析 (1)求出函数的周期,求出ω,利用图象求出A,k,然后通过函数图象经过的特殊点求出φ即可.
(2)由2k$π-\frac{π}{2}$≤2x+$\frac{π}{3}$≤2k$π+\frac{π}{2}$,k∈Z可解得f(x)的单调递增区间.
(3)由2x+$\frac{π}{3}$=kπ$+\frac{π}{2}$,k∈Z可解得函数f(x)图象的对称轴的方程,由2x+$\frac{π}{3}$=kπ,k∈Z可解得函数f(x)图象的对称中心坐标.
解答 解:(1)由函数的图象可知:A=3,k=0,T=2×($\frac{π}{12}+\frac{5π}{12}$)=π,所以ω=$\frac{2π}{T}$=2,
因为函数的图象经过($\frac{π}{12}$,3),
所以3=3sin(2×$\frac{π}{12}$+φ),即1=sin($\frac{π}{6}$+φ),
可解得:φ=2kπ+$\frac{π}{3}$,k∈Z,
因为|φ|<$\frac{π}{2}$,所以φ=$\frac{π}{3}$,
故此函数的解析式为:y=3sin(2x+$\frac{π}{3}$).
(2)由2k$π-\frac{π}{2}$≤2x+$\frac{π}{3}$≤2k$π+\frac{π}{2}$,k∈Z可解得f(x)的单调递增区间为:[kπ-$\frac{5π}{12}$,k$π+\frac{π}{12}$],k∈Z.
(3)由2x+$\frac{π}{3}$=kπ$+\frac{π}{2}$,k∈Z可解得函数f(x)图象的对称轴的方程为:x=$\frac{kπ}{2}+\frac{π}{12}$,k∈Z.
由2x+$\frac{π}{3}$=kπ,k∈Z可解得函数f(x)图象的对称中心坐标为:($\frac{kπ}{2}$-$\frac{π}{6}$,0).
点评 本题考查三角函数的解析式的求法,考查了正弦函数的图象和性质,注意函数的图象的应用,考查分析问题解决问题的能力.

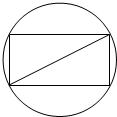 如图,把截面半径为10cm的圆形木头锯成矩形木料,如果矩形一边长为x,面积为y,试将y表表示成x的函数,并画出函数的大致图象,并判断怎样锯才能使得截面面积最大?
如图,把截面半径为10cm的圆形木头锯成矩形木料,如果矩形一边长为x,面积为y,试将y表表示成x的函数,并画出函数的大致图象,并判断怎样锯才能使得截面面积最大?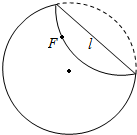 准备一张圆形纸片,在圆内任取不同于圆心的一点F,将纸片折起,使圆周过点F(如图),然后将纸片展开,就得到一条折痕L(为了看清楚,可以把直线L画出来),这样继续下去得到若干折痕.观察这些折痕围成的轮廓,它们形成了什么曲线?
准备一张圆形纸片,在圆内任取不同于圆心的一点F,将纸片折起,使圆周过点F(如图),然后将纸片展开,就得到一条折痕L(为了看清楚,可以把直线L画出来),这样继续下去得到若干折痕.观察这些折痕围成的轮廓,它们形成了什么曲线?