题目内容
6.若ab≠0,则$\frac{a}{|a|}$+$\frac{|b|}{b}$可能的取值是什么?分析 求出表达式的值,即可得到结果.
解答 解:当a<0,b<0时,$\frac{a}{|a|}$+$\frac{|b|}{b}$=-2,
当a<0,b>0时,$\frac{a}{|a|}$+$\frac{|b|}{b}$=0,
当a>0,b<0时,$\frac{a}{|a|}$+$\frac{|b|}{b}$=0,
当a>0,b>0时,$\frac{a}{|a|}$+$\frac{|b|}{b}$=2,
ab≠0,则$\frac{a}{|a|}$+$\frac{|b|}{b}$可能的取值是{-2,0.2}.
点评 本题考查表达式的值,绝对值的求法,考查计算能力.

练习册系列答案
相关题目
17.已知函数f(x)=$\left\{\begin{array}{l}{{log}_{\frac{1}{2}}x,x>1}\\{sinx,0≤x≤1}\\{\frac{x}{3},x<0}\end{array}\right.$,则下列结论中,正确的是( )
| A. | f(x)在区间(1,+∞)上是增函数 | B. | f(x)在区间(-∞,1]上是增函数 | ||
| C. | f($\frac{π}{2}$)=1 | D. | f(2)=1 |
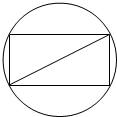 如图,把截面半径为10cm的圆形木头锯成矩形木料,如果矩形一边长为x,面积为y,试将y表表示成x的函数,并画出函数的大致图象,并判断怎样锯才能使得截面面积最大?
如图,把截面半径为10cm的圆形木头锯成矩形木料,如果矩形一边长为x,面积为y,试将y表表示成x的函数,并画出函数的大致图象,并判断怎样锯才能使得截面面积最大?