题目内容
11.由1,2,3,4,5,6等6个数可组成( )个无重复且是6的倍数的5位数.| A. | 100 | B. | 120 | C. | 240 | D. | 300 |
分析 根据题意,分析可得符合条件的5位数必须是偶数且能被3整除,首先在在1,2,3,4,5,6中任取5个,组成5位数,分析可得由其组成的5位数可以被3整除的情况有“1,2,3,4,5”、“1,2,4,5,6”2种情况,进而据此分2种情况讨论,分别求出每一种情况的5位数的个数,由分类加法原理计算可得答案.
解答 解:根据题意,若一个数是6的倍数的5位数,则它必须是偶数且能被3整除,
在1,2,3,4,5,6中任取5个,组成5位数,有C65=6种取法,
依次为“1,2,3,4,5”、“1,2,3,4,6”、“1,2,3,5,6”、“1,2,4,5,6”、“1,3,4,5,6”、“2,3,4,5,6”;
其中组成5位数可以被3整除的有“1,2,3,4,5”、“1,2,4,5,6”,共2种,
分2种情况讨论:
①、如果取出5个数字是“1,2,3,4,5”,
其个位必须是偶数,即2、4其中1个,有2种情况,
剩余4个数字安排在其余4个数位,有A44=24种情况,
则此时共有2×24=48个无重复且是6的倍数的5位数;
②、如果取出5个数字是“1,2,4,5,6”,
其个位必须是偶数,即2、4、6其中1个,有3种情况,
剩余4个数字安排在其余4个数位,有A44=24种情况,
则此时共有3×24=72个无重复且是6的倍数的5位数;
综合可得,一共有48+72=120个无重复且是6的倍数的5位数;
故选:B.
点评 本题考查排列、组合的应用,解答的关键是分析出“6的倍数”的5位数的特点,进而利用排列组合数公式进行分析.

练习册系列答案
相关题目
19.执行如图所示的程序框图,则输出的结果是( )
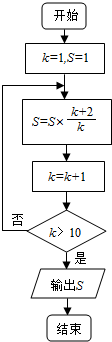

| A. | 9 | B. | 11 | C. | 55 | D. | 66 |
3.下列给出的六个函数①y=2x2;②y=2x;③y=cosx;④y=x${\;}^{\frac{1}{2}}$;⑤y=|x|;⑥y=log2x中在定义域内是偶函数,且在区间(0,+∞)内为增函数的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.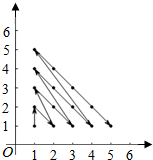 已知整数按如下规律排成一列:(1,1)、(1,2)、(2,1)、(1,3)、(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第70个数对是( )
已知整数按如下规律排成一列:(1,1)、(1,2)、(2,1)、(1,3)、(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第70个数对是( )
 已知整数按如下规律排成一列:(1,1)、(1,2)、(2,1)、(1,3)、(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第70个数对是( )
已知整数按如下规律排成一列:(1,1)、(1,2)、(2,1)、(1,3)、(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第70个数对是( )| A. | (2,11) | B. | (3,10) | C. | (4,9) | D. | (5,8) |
1.设f(x)=2|x|,则${∫}_{-2}^{4}$f(x)dx=( )
| A. | $\frac{12}{ln2}$ | B. | $\frac{20}{ln2}$ | C. | $\frac{18}{ln2}$ | D. | $\frac{16}{ln2}$ |