题目内容
【题目】已知直线l1：4x－3y＋6＝0和直线l2：x＝－
.若拋物线C：y2＝2px(p>0)上的点到直线l1和直线l2的距离之和的最小值为2.
(1)求抛物线C的方程；
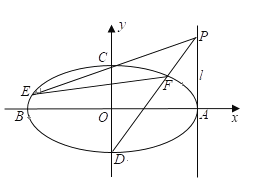
(2)若以拋物线上任意一点M为切点的直线l与直线l2交于点N，试问在x轴上是否存在定点Q，使Q点在以MN为直径的圆上，若存在，求出点Q的坐标，若不存在，请说明理由．
【答案】（1）y2＝4x（2）存在定点Q(1，0)，使Q在以MN为直径的圆上．
【解析】
试题解: （Ⅰ）由定义知
为抛物线的准线，抛物线焦点坐标
由抛物线定义知抛物线上点到直线的距离等于其到焦点F的距离.
所以抛物线上的点到直线
和直线的距离之和的最小值为焦点F到直线的距离.…………2分
所以
，则
=2,所以，抛物线方程为
.………………4分
（Ⅱ）设M
，由题意知直线
斜率存在，设为k,且
,所以直线方程为
,
代入消x得：
由
………………6分
所以直线方程为
，令x=-1,又由
得
设
则
由题意知
……………8分
，把代入左式,
得：
，……………10分
因为对任意的
等式恒成立，
所以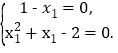
所以
即在x轴上存在定点Q（1,0）在以MN为直径的圆上.……………12分
练习册系列答案
名校课堂系列答案
相关题目
