题目内容
【题目】已知椭圆![]() 的离心率
的离心率![]() ,且经过点
,且经过点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为椭圆的四个顶点(如图),直线
为椭圆的四个顶点(如图),直线![]() 过右顶点
过右顶点![]() 且垂直于
且垂直于![]() 轴.
轴.
(1)求该椭圆的标准方程;
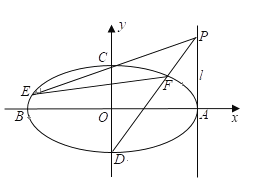
(2)![]() 为
为![]() 上一点(
上一点(![]() 轴上方),直线
轴上方),直线![]() ,
,![]() 分别交椭圆于
分别交椭圆于![]() ,
,![]() 两点,若
两点,若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)利用椭圆的离心率和经过的点![]() ,列方程组求解即可.(2)设P(2,m),m>0,得直线PC方程与椭圆联立,利用韦达定理,推出E的坐标, 同理求F点横坐标,由S△PCD=2S△PEF,转化求解即可.
,列方程组求解即可.(2)设P(2,m),m>0,得直线PC方程与椭圆联立,利用韦达定理,推出E的坐标, 同理求F点横坐标,由S△PCD=2S△PEF,转化求解即可.
(1)因![]() 的离心率
的离心率![]() ,且经过点
,且经过点![]() ,
,
所以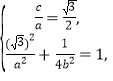
解得![]() ,
,![]() .所以椭圆标准方程为
.所以椭圆标准方程为![]() .
.
(2)由(1)知椭圆方程为![]() ,所以直线
,所以直线![]() 方程为
方程为![]() ,
,![]() ,
,![]() .
.
设![]() ,
,![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
联立方程组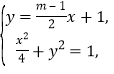 消
消![]() 得
得![]() ,
,
所以![]() 点的横坐标为
点的横坐标为![]() ;
;
又直线![]() 的方程为
的方程为![]()
联立方程组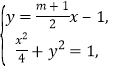 消
消![]() 得
得![]() ,
,
所以![]() 点的横坐标为
点的横坐标为![]() .
.
由![]() 得
得![]() ,
,
则有![]() ,则
,则![]() ,
,
化简得![]() ,解得
,解得![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
所以点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

