题目内容
【题目】已知函数
．
(1)求
的单调区间；
(2)设
，若
，均
，使得
，求
的取值范围．
【答案】(1)见解析；(2) 
【解析】
（1）求出函数的导数，通过讨论a的范围，求出函数的单调区间即可；
（2）问题转化为
，，分别求出其最大值，得到关于a的不等式，解出即可．
（1）
.
当
时，由
，得
，
，
∴函数
的递减区间是
；
当
时，由
得
，
∴当
时，
；当
时，.
∴函数的递增区间是
，递减区间是
；
综上，当时，函数的递减区间是；
当时，函数的递增区间是，递减区间是.
（2）依题意，要满足对任意
，均存在
，使得
，
只需满足，
∵
，
，∴
由（1）知，
当
时，函数在区间上单调递减，值域为
，不符合题意；
当
时，
，符合题意；
当时，函数在区间上递增，在区间上递减，
∴
，
令
，解得
；
综上，
的取值范围是.
练习册系列答案
相关题目
【题目】某市2011年至2017年新开楼盘的平均销售价格(单位：千元/平方米)的统计数据如下表：
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格 | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
（1）求
关于x的线性回归方程；
（2）利用（1）中的回归方程，分析2011年至2017年该市新开楼盘平均销售价格的变化情况，并预测该市2019年新开楼盘的平均销售价格。
附：参考公式：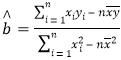 
，
，其中
为样本平均值。
参考数据：
．
