题目内容
【题目】已知函数![]() 为定义在
为定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时,![]() .
.
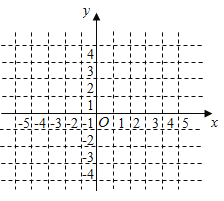
(1)求当![]() 时,
时,![]() 的解析式;
的解析式;
(2)在网格中绘制![]() 的图像;
的图像;
(3)若方程![]() 有四个根,求
有四个根,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ; (2)见解析; (3)
; (2)见解析; (3)![]() .
.
【解析】
(1)设![]() ,则
,则![]() ,由函数
,由函数![]() 为定义在
为定义在![]() 上的偶函数,求得
上的偶函数,求得![]() ,即可得到答案;
,即可得到答案;
(2)由(1)可得函数的解析式为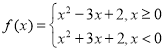 ,根据二次函数的图象与性质,即可得到函数的图象.
,根据二次函数的图象与性质,即可得到函数的图象.
(3)要使得方程![]() 有四个根,即函数
有四个根,即函数![]() 与
与![]() 的图象有4个不同的交点,结合图象,即可求解.
的图象有4个不同的交点,结合图象,即可求解.
(1)由题意,设![]() ,则
,则![]() ,
,
因为函数![]() 为定义在
为定义在![]() 上的偶函数,
上的偶函数,
所以![]() ,
,
即当![]() 时,
时,![]() .
.
(2)由(1)可得函数的解析式为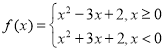 ,
,
函数的图象如图所示:
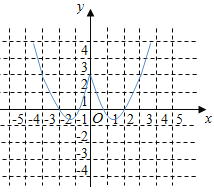
(3)由(2)可得,当![]() 时,
时,![]() ,
,
当![]() 或
或![]() 时,可得
时,可得![]() ,
,
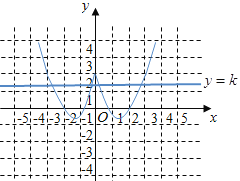
要使得方程![]() 有四个根,即函数
有四个根,即函数![]() 与
与![]() 的图象有4个不同的交点,
的图象有4个不同的交点,
如图所示,则满足![]() ,
,
即![]() 的取值范围
的取值范围![]() .
.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目