题目内容

【题目】已知椭圆长轴是短轴的倍，且右焦点为.

（Ⅰ）求椭圆C的标准方程；

（Ⅱ）直线交椭圆于两点，若线段中点的横坐标为，求直线的方程及的面积.

【答案】（Ⅰ）（Ⅱ）1

【解析】

（I）根据焦点坐标求得，根据长轴和短轴的对应关系，以及列方程组，可求得的值，进而求得椭圆的标准方程.（II）联立直线的方程和椭圆的方程，消去并化简，写出韦达定理，根据中点的横坐标求得的值.利用弦长公式求得，利用点到直线的距离公式求得焦点到直线的距离，由此求得三角形的面积.

（Ⅰ）因为长轴是短轴的倍，所以.

因为焦点的坐标为，所以.

结合，得.

所以椭圆方程为.

（Ⅱ）设，.

由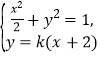得.

则.

因为线段中点的横坐标为，

所以 .

解得 ，即（符合题意）

所以直线的方程为，

因为 .

点到直线的距离.

所以的面积 .

即的面积等于.

练习册系列答案
相关题目

【题目】已知函数.

（1）若函数为偶函数，求实数的值；

（2）若，求函数的单调递减区间；

（3）当时，若对任意的，不等式恒成立，求实数的取值范围.

【题目】已知直线l1：4x－3y＋6＝0和直线l2：x＝－.若拋物线C：y2＝2px(p>0)上的点到直线l1和直线l2的距离之和的最小值为2.

(1)求抛物线C的方程；

(2)若以拋物线上任意一点M为切点的直线l与直线l2交于点N，试问在x轴上是否存在定点Q，使Q点在以MN为直径的圆上，若存在，求出点Q的坐标，若不存在，请说明理由．

【题目】某学校团委组织了“文明出行，爱我中华”的知识竞赛，从参加考试的学生中抽出60名学生，将其成绩（单位：分）整理后，得到如下频率分布直方图（其中分组区间为，，…，）.

（1）求成绩在的频率，并补全此频率分布直方图；

（2）求这次考试平均分的估计值；

（3）若从成绩在和的学生中任选两人，求他们的成绩在同一分组区间的概率.

【题目】关于的方程的实根个数记.（1）若，则=____________；（2）若，存在使得成立，则的取值范围是_____.

【题目】已知为实数，数列满足，.

（Ⅰ）当和时，分别写出数列的前5项；

（Ⅱ）证明：当时，存在正整数，使得；

（Ⅲ）当时，是否存在实数及正整数，使得数列的前项和？若存在，求出实数及正整数的值；若不存在，请说明理由.

【题目】已知函数f(x)＝log4(4x＋1)＋kx(k∈R)是偶函数．

(1)求k的值；

(2)设g(x)＝log4，若函数f(x)与g(x)的图象有且只有一个公共点，求实数a的取值范围．

【题目】已知定义域是R上的奇函数．

（1）求a；

（2）判断在R上的单调性，并用定义法证明；

（3）若对任意的，不等式恒成立，求实数k的取值范围；

（4）设关于x方程有零点，求实数b的取值范围．

【题目】已知椭圆的离心率为，其左、右焦点为F1、F2，点P是坐标平面内一点，且其中O为坐标原点。

（I） 求椭圆C的方程；

（II） 如图，过点S（0，}，且斜率为k的动直线l交椭圆于A、B两点，在y轴上是否存在定点M，使以AB为直径的圆恒过这个点？若存在，求出点M的坐标；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网