题目内容
【题目】已知F1 , F2分别是椭圆C: ![]() =1(a>b>0)的两个焦点,P(1,
=1(a>b>0)的两个焦点,P(1, ![]() )是椭圆上一点,且
)是椭圆上一点,且 ![]() |PF1|,|F1F2|,
|PF1|,|F1F2|, ![]() |PF2|成等差数列.
|PF2|成等差数列.
(1)求椭圆C的标准方程;
(2)已知动直线l过点F2 , 且与椭圆C交于A、B两点,试问x轴上是否存在定点Q,使得 ![]() =﹣
=﹣ ![]() 恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】
(1)解:∵ ![]() |PF1|,|F1F2|,
|PF1|,|F1F2|, ![]() |PF2|成等差数列,
|PF2|成等差数列,
∴ ![]() |PF1|+
|PF1|+ ![]() |PF2|=2|F1F2|,即2
|PF2|=2|F1F2|,即2 ![]() a=4c,∴a=
a=4c,∴a= ![]() .
.
∴ 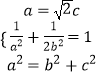 ,解得
,解得 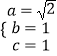 .
.
∴椭圆方程为 ![]() .
.
(2)解:假设在x轴上存在点Q(m,0),使得 ![]() 恒成立.
恒成立.
① 当直线l的斜率为0时,A(﹣ ![]() ,0),B(
,0),B( ![]() ,0).
,0).
∴ ![]() =(﹣
=(﹣ ![]() ﹣m,0),
﹣m,0), ![]() =(
=( ![]() ﹣m,0).
﹣m,0).
∴ ![]() =m2﹣2=﹣
=m2﹣2=﹣ ![]() ,解得
,解得 ![]() 或m=﹣
或m=﹣ ![]() .
.
②若直线l斜率不为0,设直线AB的方程为x=ty+1.
联立方程组 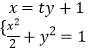 ,消元得:(t2+2)y2+2ty﹣1=0.
,消元得:(t2+2)y2+2ty﹣1=0.
设A(x1,y1),B(x2,y2),则y1+y2=﹣ ![]() ,y1y2=﹣
,y1y2=﹣ ![]() .
.
∴x1+x2=t(y1+y2)+2= ![]() ,
,
x1x2=(ty1+1)(ty2+1)=t2y1y2+t(y1+y2)+1= ![]() .
.
∵ ![]() =(x1﹣m,y1),
=(x1﹣m,y1), ![]() =(x2﹣m,y2).
=(x2﹣m,y2).
∴ ![]() =(x1﹣m)(x2﹣m)+y1y2=x1x2﹣m(x1+x2)+m2+y1y2
=(x1﹣m)(x2﹣m)+y1y2=x1x2﹣m(x1+x2)+m2+y1y2
= ![]() ﹣
﹣ ![]() +m2﹣
+m2﹣ ![]() =
= ![]() =﹣
=﹣ ![]() .
.
∴ 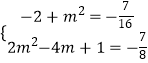 ,解得m=
,解得m= ![]() .
.
综上,Q点坐标为( ![]() ,0)
,0)
【解析】(1)根据椭圆的性质及等差数列性质得出a= ![]() c,把P点坐标代入椭圆方程列方程组解出a,b得出椭圆方程;(2)设Q(m,0),当直线斜率为0时,求出A,B坐标,列方程解出m,当直线斜率不为0时,设AB方程为x=ty+1,联立方程组得出A,B坐标的关系,根据
c,把P点坐标代入椭圆方程列方程组解出a,b得出椭圆方程;(2)设Q(m,0),当直线斜率为0时,求出A,B坐标,列方程解出m,当直线斜率不为0时,设AB方程为x=ty+1,联立方程组得出A,B坐标的关系,根据 ![]() =﹣
=﹣ ![]() 列方程解出m.
列方程解出m.