题目内容
(本小题满分14分)已知在函数 的图象上以N(1,n)为切点的切线的倾斜角为
的图象上以N(1,n)为切点的切线的倾斜角为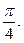
(1)求m、n的值;
 (2)是否存在最小的正整数k,使得不等式
(2)是否存在最小的正整数k,使得不等式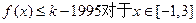 恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
(3 )求证:
)求证: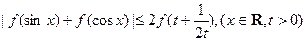 .
.
 的图象上以N(1,n)为切点的切线的倾斜角为
的图象上以N(1,n)为切点的切线的倾斜角为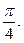
(1)求m、n的值;
 (2)是否存在最小的正整数k,使得不等式
(2)是否存在最小的正整数k,使得不等式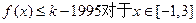 恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;(3
 )求证:
)求证: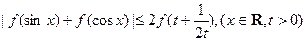 .
.(1)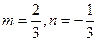 ;(2)k=2010;(3)略
;(2)k=2010;(3)略
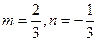 ;(2)k=2010;(3)略
;(2)k=2010;(3)略(1)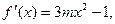 依题意,得
依题意,得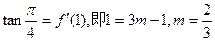
∴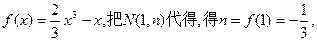
∴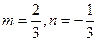 …………………………………………………………(4分)
…………………………………………………………(4分)
(2)令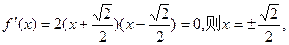
当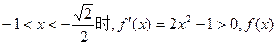 在此区间为增函数
在此区间为增函数
当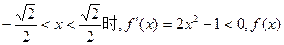 在此区间为减函数
在此区间为减函数
当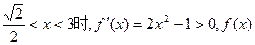 在此区间为增函数
在此区间为增函数
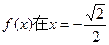 处取得极大值 ……………………………………………6分
处取得极大值 ……………………………………………6分
又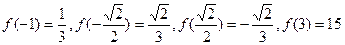
因此,当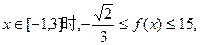 ………………………………8分
………………………………8分
要使得不等式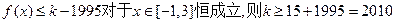
所以,存在最小的正整数k=2010,
使得不等式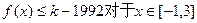 恒成立. ……………………10分
恒成立. ……………………10分
(3)(方法一)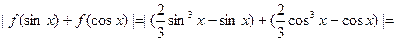


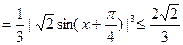 ……………………………………………12分
……………………………………………12分
又∵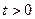 ∴
∴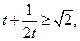 由(2)知
由(2)知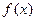 在
在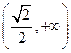 为增函数,
为增函数,
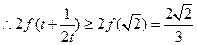
综上可得: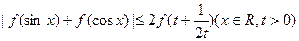 ………………14分
………………14分
(方法2)由(2)知,函数
上是减函数,在[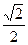 ,1]上是增函数
,1]上是增函数
又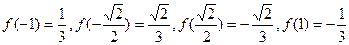
所以,当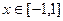 时,-
时,-
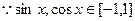
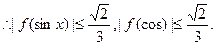
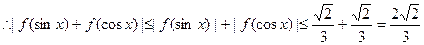 ………12分
………12分
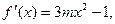 依题意,得
依题意,得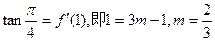
∴
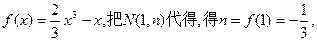
∴
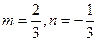 …………………………………………………………(4分)
…………………………………………………………(4分)(2)令
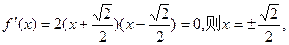
当
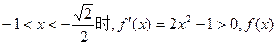 在此区间为增函数
在此区间为增函数当
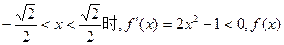 在此区间为减函数
在此区间为减函数当
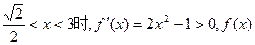 在此区间为增函数
在此区间为增函数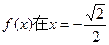 处取得极大值 ……………………………………………6分
处取得极大值 ……………………………………………6分又
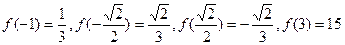
因此,当
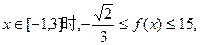 ………………………………8分
………………………………8分要使得不等式
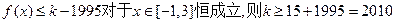
所以,存在最小的正整数k=2010,
使得不等式
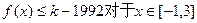 恒成立. ……………………10分
恒成立. ……………………10分(3)(方法一)
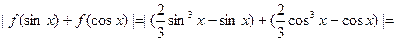


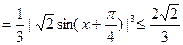 ……………………………………………12分
……………………………………………12分又∵
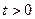 ∴
∴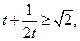 由(2)知
由(2)知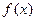 在
在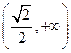 为增函数,
为增函数,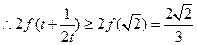
综上可得:
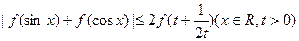 ………………14分
………………14分(方法2)由(2)知,函数

上是减函数,在[
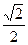 ,1]上是增函数
,1]上是增函数又
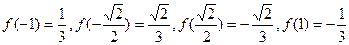
所以,当
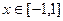 时,-
时,-
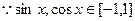
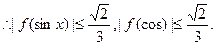
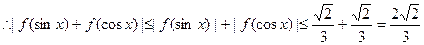 ………12分
………12分
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
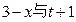 成反比例,如果不搞促销活动,化妆品的年销量只能是1万件,已知2010年生产化妆品的设备折旧、维修等固定费用为3万元,每生产1万件化妆品需要再投入32万元的生产费用,若将每件化妆品的售价定为:其生产成本的150%与平均每件促销费的一半之和,则当年生产的化妆品正好能销完。
成反比例,如果不搞促销活动,化妆品的年销量只能是1万件,已知2010年生产化妆品的设备折旧、维修等固定费用为3万元,每生产1万件化妆品需要再投入32万元的生产费用,若将每件化妆品的售价定为:其生产成本的150%与平均每件促销费的一半之和,则当年生产的化妆品正好能销完。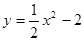 在点
在点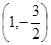 处的切线的倾斜角为
处的切线的倾斜角为



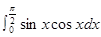 等于
等于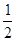
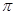
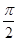
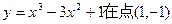 处的切线方程为( )
处的切线方程为( )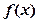 的导函数为
的导函数为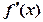 ,且满足
,且满足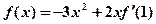 ,则
,则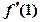 =( )
=( )
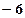
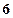
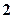
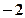
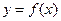 的图象在点
的图象在点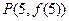 处的切线方程是
处的切线方程是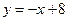 ,则
,则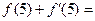 ( )
( )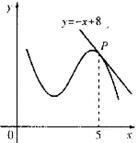
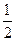

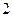
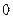
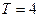 为周期的函数
为周期的函数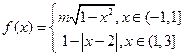 ,其中
,其中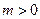 。若方程
。若方程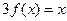 恰有5个实数解,则
恰有5个实数解,则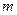 的取值范围为
的取值范围为 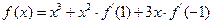 ,则
,则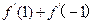 =
=