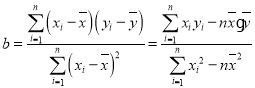题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 在区间
在区间![]() 上为减函数,求实数
上为减函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;(2)
;(2)![]()
【解析】
(1)当![]() 时,直接对
时,直接对![]() 求导,利用导数研究函数的单调性,解不等式
求导,利用导数研究函数的单调性,解不等式![]() 和
和![]() ,即可求出
,即可求出![]() 的单调区间;
的单调区间;
(2)根据函数![]() 在区间
在区间![]() 上为减函数,利用分离参数法,得出
上为减函数,利用分离参数法,得出![]() 对
对![]() 恒成立,构造函数
恒成立,构造函数![]() ,根据导数确定
,根据导数确定![]() 在区间
在区间![]() 上的单调性,从而求出
上的单调性,从而求出![]() ,即可得出实数
,即可得出实数![]() 的取值范围.
的取值范围.
解:(1)由题可知,![]() ,
,![]() 的定义域为
的定义域为![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,
令![]() ,而
,而![]() ,则
,则![]() ,解得:
,解得:![]() ,
,
令![]() ,而
,而![]() ,则
,则![]() ,解得:
,解得:![]() ,
,
![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
(2)由于![]() ,
,![]() 的定义域为
的定义域为![]() ,
,
因为函数![]() 在区间
在区间![]() 上为减函数,
上为减函数,
![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,
恒成立,
令![]() ,则
,则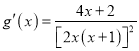 ,
,
可知,当![]() 时,
时,![]() ,即
,即![]() ,
,
即在区间![]() 上
上![]() ,故
,故![]() 在区间
在区间![]() 上单调递增,
上单调递增,
则![]() ,
,
所以![]() ,
,
即实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某研究机构对某校高二文科学生的记忆力x和判断力y进行统计分析,得下表数据.
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(3)试根据(2)中求出的线性回归方程,预测记忆力为14的学生的判断力.