题目内容
【题目】证明:任何一个正方形均可分割成![]() 个全等的非矩形图形,其中,
个全等的非矩形图形,其中,![]() 、
、![]() 为互不相等的素数.
为互不相等的素数.
【答案】见解析
【解析】
若存在一个矩形可分割成![]() 个全等的非矩形图形,则可通过倍长这个矩形的两边长将其拉伸成一个正方形.
个全等的非矩形图形,则可通过倍长这个矩形的两边长将其拉伸成一个正方形.
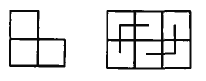
此时,可考虑用较简单的“角形”(如图4)来分割该矩形.
因此,只需说明存在![]() 个角形拼成的矩形,也就是说存在一个面积为
个角形拼成的矩形,也就是说存在一个面积为![]() 的矩形可完全分割成角形即可,不妨设
的矩形可完全分割成角形即可,不妨设![]() .
.
当![]() 时,对任意的素数
时,对任意的素数![]() ,必存在一个面积为
,必存在一个面积为![]() 的矩形可分割成角形(由
的矩形可分割成角形(由![]() 个
个![]() 的矩形并排组成的矩形),即任何一个正方形可分割成
的矩形并排组成的矩形),即任何一个正方形可分割成![]() 个全等的非矩形图形.
个全等的非矩形图形.
当![]() 时,只需说明存在一个面积为
时,只需说明存在一个面积为![]() 的矩形可分割成角形即可.
的矩形可分割成角形即可.
先将一个![]() 的矩形分割成15个角形(如图5),称该矩形为“基本矩形”.
的矩形分割成15个角形(如图5),称该矩形为“基本矩形”.
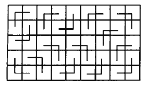
(1)若![]() ,
,![]() ,其基本矩形就是它的分割.故命题成立.
,其基本矩形就是它的分割.故命题成立.
若![]() ,
,![]() ,由
,由![]() 为素数,知
为素数,知![]() 为奇数.
为奇数.
此时,只需在基本矩形下添若干行![]() 的矩形即可,而每个
的矩形即可,而每个![]() 的矩形是由三个
的矩形是由三个![]() 的矩形并排而成,可分割成角形.故命题成立.
的矩形并排而成,可分割成角形.故命题成立.
(2)若![]() ,由(1),知可用角形拼成一个
,由(1),知可用角形拼成一个![]() 的矩形.
的矩形.
由于![]() ,又
,又![]() 为奇素数,
为奇素数,![]() 为
为![]() 的倍数,因此,可在原
的倍数,因此,可在原![]() 的矩形右侧添加若干个
的矩形右侧添加若干个![]() 的矩形,而每个
的矩形,而每个![]() 的矩形可分割成角形,它们一起构成一个面积为
的矩形可分割成角形,它们一起构成一个面积为![]() 的矩形.
的矩形.
故命题成立.
综上,对任意的素数![]() 、
、![]() ,均存在一个矩形,可将其分割成
,均存在一个矩形,可将其分割成![]() 个角形.
个角形.
从而,任何一个正方形均可分割成![]() 个全等的非矩形图形,其中,
个全等的非矩形图形,其中,![]() 、
、![]() 为互不相等的素数.
为互不相等的素数.

练习册系列答案
相关题目
【题目】在一次飞机航程中,调查男女晕机情况,在80名男乘客中有10人晕机,70人不晕机.在30名女乘客中有10人晕机,20人不晕机
(1)请根据题设数据列出![]() 列联表
列联表
晕机 | 不晕机 | 总计 | |
男 | |||
女 | |||
总计 |
(2)是否有![]() 把握认为“是否晕机与性别有关”.
把握认为“是否晕机与性别有关”.
附:![]()
| 0.050 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |