题目内容
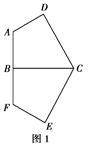
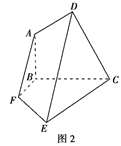
【题目】已知平面五边形![]() 是轴对称图形(如图1),BC为对称轴,AD⊥CD,AD=AB=1,
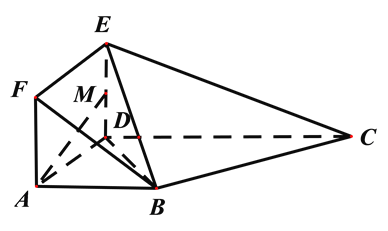
是轴对称图形(如图1),BC为对称轴,AD⊥CD,AD=AB=1,![]() ,将此五边形沿BC折叠,使平面ABCD⊥平面BCEF,得到如图2所示的空间图形,对此空间图形解答下列问题.
,将此五边形沿BC折叠,使平面ABCD⊥平面BCEF,得到如图2所示的空间图形,对此空间图形解答下列问题.
(1)证明:AF∥平面DEC;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析,(2)![]()
【解析】
试题分析:(1)作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .由已知条件得
.由已知条件得![]() .所以
.所以![]() 面
面![]() .同理:
.同理:![]() 面
面![]() .由此能证明
.由此能证明![]() 平面AFB. (2)过G作GH⊥AD于点H,连接HE.由(1)知EG⊥BC,又平面ABCD⊥平面BCEF,平面ABCD∩平面BCEF=BC,所以EG⊥平面ABCD,所以EG⊥AD.可得AD⊥平面EHG,则AD⊥HE,则∠EHG即为二面角
平面AFB. (2)过G作GH⊥AD于点H,连接HE.由(1)知EG⊥BC,又平面ABCD⊥平面BCEF,平面ABCD∩平面BCEF=BC,所以EG⊥平面ABCD,所以EG⊥AD.可得AD⊥平面EHG,则AD⊥HE,则∠EHG即为二面角![]() 的平面角. 在
的平面角. 在![]() 中,即可求出二面角
中,即可求出二面角![]() 的余弦值.
的余弦值.
试题解析:
(1)如图,过D作DG⊥BC于点G,连接GE,
因为BC为对称轴,所以AB⊥BC,则有AB∥DG,又AB平面ABF,
所以DG∥平面ABF,同理EG∥平面ABF.又DG∩EG=G,所以平面DGE∥平面ABF.
又平面AFED∩平面ABF=AF,平面AFED∩平面DGE=DE,所以AF∥DE,
又DE平面DEC,所以AF∥平面DEC.
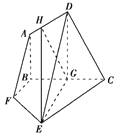
(2)如图,过G作GH⊥AD于点H,连接HE.由(1)知EG⊥BC,又平面ABCD⊥平面BCEF,平面ABCD∩平面BCEF=BC,所以EG⊥平面ABCD,所以EG⊥AD.
又EG∩HG=G,所以AD⊥平面EHG,则AD⊥HE,
则∠EHG即为二面角![]() 的平面角.
的平面角.
由AD⊥CD,AD=AB=1,![]() ,得G为BC的中点,
,得G为BC的中点,![]() ,
,![]() ,
,![]() .
.
因为![]() 为直角三角形,所以
为直角三角形,所以![]() ,
,
则二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目