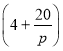题目内容
【题目】设点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,直线
,直线![]() 和
和![]() 相交于点
相交于点![]() ,且
,且![]() 和
和![]() 的斜率之差是1.
的斜率之差是1.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过轨迹![]() 上的点
上的点![]() ,
,![]() ,作圆
,作圆![]() :
:![]() 的两条切线,分别交
的两条切线,分别交![]() 轴于点
轴于点![]() ,
,![]() .当
.当![]() 的面积最小时,求
的面积最小时,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)设出![]() 点坐标,根据
点坐标,根据![]() 和
和![]() 的斜率之差是
的斜率之差是![]() 列方程,化简后求得点
列方程,化简后求得点![]() 的轨迹
的轨迹![]() 的方程.注意排除斜率不存在的情况.
的方程.注意排除斜率不存在的情况.
(2)设出切线的斜率,由点斜式写出切线方程,利用圆心![]() 到切线的距离为
到切线的距离为![]() 列方程,化简后写出关于切线
列方程,化简后写出关于切线![]() 、
、![]() 的斜率
的斜率![]() ,
,![]() 的根与系数关系,求得
的根与系数关系,求得![]() 两点的坐标,进而求得
两点的坐标,进而求得![]() 的面积的表达式,化简后利用基本不等式求得
的面积的表达式,化简后利用基本不等式求得![]() 的面积的最小值以及此时对应
的面积的最小值以及此时对应![]() 的值.
的值.
(1)设![]() ,由题意得
,由题意得![]() .
.
化简得点![]() 的轨迹
的轨迹![]() 的方程为:
的方程为:![]() .
.
(2)由点![]() 所引的切线方程必存在斜率,设为
所引的切线方程必存在斜率,设为![]() .
.
则切线方程为![]() ,即
,即![]() .
.
其与![]() 轴的交点为
轴的交点为![]() ,
,
而圆心![]() 到切线的距离
到切线的距离![]() ,
,
整理得:![]() ①,
①,
切线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,则
,则![]() ,
,![]() 是方程①的两根,
是方程①的两根,
故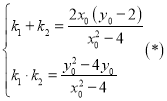 ,
,
而切线与![]() 轴的交点为
轴的交点为![]() ,故
,故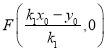 ,
,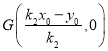 ,
,
又![]() ,
,![]() ,
,
∴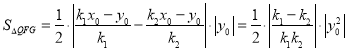
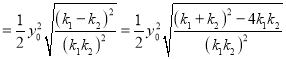 ,
,
将![]() 代入得
代入得
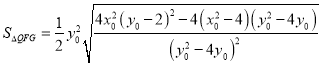
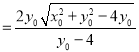 ,
,
而点![]() 在
在![]() 上,故
上,故![]() ,
,
∴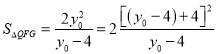
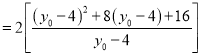
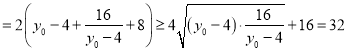 ,
,
当且仅当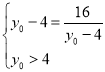 ,即
,即![]() 时等号成立.
时等号成立.
又![]() ,∴
,∴![]() ,
,
故当点![]() 坐标为
坐标为![]() ,
,![]() 时,
时,![]() .
.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目