题目内容
9．
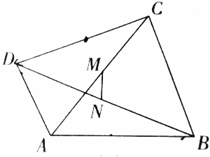如图，四边形ABCD的对角线AC、BD的中点分别为M、N，求证：$\frac{1}{2}$|AB-CD|≤MN≤$\frac{1}{2}$（AB+CD）．
分析 利用三角形的中位线以及三角形三边关系得到所求．
解答 解：过M作ME∥AB，因为对角线AC、BD的中点分别为M、N，则E为BC的中点，连接NE，
则NE∥CD，
在△MNE中，根据三角形三边关系得到
MN＜ME+NE=$\frac{1}{2}$（AB+CD），
MN＞|ME-NE|=$\frac{1}{2}$|AB-CD|，
所以：$\frac{1}{2}$|AB-CD|≤MN≤$\frac{1}{2}$（AB+CD）．
点评 本题考查了三角形的中位线以及三角形三边关系．
练习册系列答案
相关题目
20．已知集合 A={x∈R|x-1≥0}，B={x∈R||x|≤2}，则A∩B=（ ）
| A． | {x∈R|-2≤x≤2} | B． | {x∈R|-1≤x≤2} | C． | {x∈R|1≤x≤2} | D． | {x∈R|-1≤x≤1} |
17．已知实数x，y满足条件$\left\{\begin{array}{l}2x+y≥4\\ x-y≥1\\ x-2y≤2\end{array}\right.$，则z=x+2y的最小值为（ ）
| A． | $\frac{4}{3}$ | B． | 4 | C． | 2 | D． | 3 |
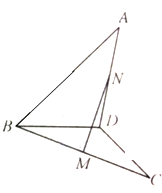如图，在空间四边形ABCD中，AB=CD=8，M，N分别是BC，AD的中点，若异面直线AB与CD所成的角为60°时，求MN的长．
某同学做了一个如图所示的等腰直角三角形形状的数表，且把奇数和偶数分别依次排在了数表的奇数行和偶数行，若用a（i，j）表示第i行从左数第j个数，如a（4，3）=10，则a（21，6）=（ ）
如图，在斜三棱柱ABC-A1B1C1中，侧面AA1B1B⊥底面ABC，侧棱AA1与底面ABC成60°的角，AA1=2，底面ABC是边长为2的正三角形，其重心为G点，E是线段BC1上一点，且$BE=\frac{1}{3}B{C_1}$．