题目内容
设抛物线y2=2px(p＞0)被直线y=2x-4截得的弦AB长为3
．
（1）求此抛物线的方程；
（2）设直线AB上有一点Q，使得A，Q，B三点到抛物线准线的距离成等差数列，求Q点坐标；
（3）在抛物线上求一点M，使M到Q点距离与M到焦点的距离之和最小．
| 5 |
（1）求此抛物线的方程；
（2）设直线AB上有一点Q，使得A，Q，B三点到抛物线准线的距离成等差数列，求Q点坐标；
（3）在抛物线上求一点M，使M到Q点距离与M到焦点的距离之和最小．
（1）联立方程组，得
，整理得：2x2-（8+p）x+8=0
设A（x1，y1），B（x2，y2），
则x1+x2=
，x1x2=4，
∴弦长AB=
=3
，
解得p=2或-18（舍），
所以此抛物线的方程：y2=4x．
（2）设Q（x，y），
∵A，Q，B三点到抛物线准线的距离成等差数列，
∴x=
=
=
，
∴y=2×
-4=1，
∴Q(
，1)．
（3）∵M到Q点距离与M到焦点的距离之和最小值是Q到准线的距离，
∴M点的纵坐标是y=1，
把y=1代入y2=4x，得x=
，
∴M(
，1)．
|
设A（x1，y1），B（x2，y2），
则x1+x2=
| 8+p |
| 2 |
∴弦长AB=
(1+4)[(
|
| 5 |
解得p=2或-18（舍），
所以此抛物线的方程：y2=4x．
（2）设Q（x，y），
∵A，Q，B三点到抛物线准线的距离成等差数列，
∴x=
| x1+y1 |
| 2 |
| ||
| 2 |
| 5 |
| 2 |
∴y=2×
| 5 |
| 2 |
∴Q(
| 5 |
| 2 |
（3）∵M到Q点距离与M到焦点的距离之和最小值是Q到准线的距离，
∴M点的纵坐标是y=1，
把y=1代入y2=4x，得x=
| 1 |
| 4 |
∴M(
| 1 |
| 4 |
练习册系列答案
一线名师提优试卷系列答案
相关题目
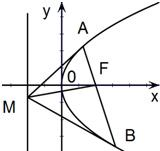设抛物线y2=2px（p＞0）的焦点为F，经过点F的直线交抛物线于A，B两点，且A，B两点坐标分别为（x1，y1）、（x2，y2），y1＞0，y2＜0，M是抛物线的准线上的一点，O是坐标原点．若直线MA，MF，MB的斜率分别记为：KMA=a，KMF=b，KMB=c，（如图）