题目内容
7、设抛物线y2=2px（p＞0）上一点A（1，2）到点B（x0，0）的距离等于到直线x=-1的距离，则实数x0的值是
1
．分析：把点A坐标代入抛物线方程 求得 p，即能确定抛物线方程，准线方程及焦点坐标，由条件，并结合抛物线的定义，可得B（x0，0）为抛物线 y2=4x 的焦点，从而求得x0 的值．
解答：解：∵点A（1，2）在抛物线y2=2px（p＞0）上，∴4=2p，p=2，
故抛物线方程为 y2=4x，准线方程为 x=1．由点A（1，2）到点B（x0，0）的距离等于到直线x=-1的距离，
故点B（x0，0）为抛物线 y2=4x 的焦点，故x0=1．
故答案为 1．
故抛物线方程为 y2=4x，准线方程为 x=1．由点A（1，2）到点B（x0，0）的距离等于到直线x=-1的距离，
故点B（x0，0）为抛物线 y2=4x 的焦点，故x0=1．
故答案为 1．
点评：本题考查抛物线的定义、标准方程，以及简单性质的应用，判断点B（x0，0）为抛物线 y2=4x 的焦点，是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
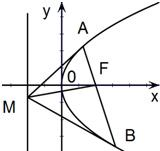设抛物线y2=2px（p＞0）的焦点为F，经过点F的直线交抛物线于A，B两点，且A，B两点坐标分别为（x1，y1）、（x2，y2），y1＞0，y2＜0，M是抛物线的准线上的一点，O是坐标原点．若直线MA，MF，MB的斜率分别记为：KMA=a，KMF=b，KMB=c，（如图）