Question

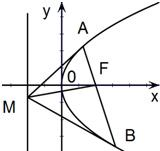设抛物线y²=2px（p＞0）的焦点为F，经过点F的直线交抛物线于A，B两点，且A，B两点坐标分别为（x₁，y₁）、（x₂，y₂），y₁＞0，y₂＜0，M是抛物线的准线上的一点，O是坐标原点．若直线MA，MF，MB的斜率分别记为：K_MA=a，K_MF=b，K_MB=c，（如图）
（I）若y₁y₂=-4，求抛物线的方程；
（II）当b=2时，求a+c的值；
（III）如果取KMA=2，KMB=-

1

2

时，判定|∠AMF-∠BMF|和∠MFO的值大小关系．并说明理由．

Answer 1

分析：（I）设直线AB的方程为y=k(x-

p

2

)，由

y=k(x- p 2 ) y2=2px

得

k

2p

y2-y-

kp

2

=0，由此能求出抛物线的方程．
（II）设M(-

p

2

，y0)则b=

y0

- p 2 - p 2

=2，所以y₀=-2p，由此能够推导出a+c=

8p2

2p2

=4．
（III）设直线AM、FM、BM的倾斜角分别为θ₁，θ₂，θ₃，则∠AMF=θ₁-θ₂，∠BMF=θ₃+θ₂，∠MFO=θ₂，tanθ1=2，tanθ3=-

1

2

，由此能够导出|∠AMF-∠BMF|＞∠MFO．

解答：解：（I）设直线AB的方程为y=k(x-

p

2

)
由

y=k(x- p 2 ) y2=2px

消去x得

k

2p

y2-y-

kp

2

=0
所以y₁y₂=-p²=-4
因为p＞0，所以p=2
所以此抛物线的方程为y²=4x
（II）设M(-

p

2

，y0)则b=

y0

- p 2 - p 2

=2，所以y₀=-2p
所以a+c=

y1+2p

x1+ p 2

+

y2+2p

x2+ p 2

=

y1+2p

1 k y1+p

+

y1+2p

1 k y1+p

=

2ky1y2+pk(2+k)(y1+y2)+4p2

y1y2+pk(y1+y2)+p2

由（*）得y₁y₂=-p²，(y1+y2)=

2p

k

所以a+c=

8p2

2p2

=4
（III）设直线AM、FM、BM的倾斜角分别为θ₁，θ₂，θ₃，
则∠AMF=θ₁-θ₂，∠BMF=θ₃+θ₂，∠MFO=θ₂tanθ1=2，tanθ3=-

1

2

所以θ₁+θ₃=

π

2

所以|∠AMF-∠BMF|＞∠MFO

点评：本题主要考查直线与圆锥曲线的综合应用能力，具体涉及到轨迹方程的求法及直线与抛物线的相关知识，解题时要注意合理地进行等价转化．