题目内容
设抛物线y2=2px(p>0)的焦点为F,其准线与x轴的交点为Q,过Q点的直线l交抛物线于A,B两点.
(1)若直线l的斜率为
,求证:
•
=0;
(2)设直线FA,FB的斜率分别为k1,k2,求k1+k2的值.
(1)若直线l的斜率为
| ||
| 2 |
| FA |
| FB |
(2)设直线FA,FB的斜率分别为k1,k2,求k1+k2的值.
分析:(1)由点斜式写出直线l的方程,和抛物线方程联立后化为关于x的一元二次方程,利用根与系数关系求出A,B两点的横坐标的和与积,写出向量
,
的坐标,展开数量积后代入根与系数关系得答案;
(2)设直线l的方程为l:x=ky-
,和抛物线方程联立后话诶关于y的一元二次方程,写出根与系数关系,由两点式求出斜率后作和化简,代入根与系数关系即可得到答案.
| FA |
| FB |
(2)设直线l的方程为l:x=ky-
| p |
| 2 |
解答:(1)证明:由题意可得l:y=
(x+
),
联立
,得x2-3px+
=0.
设A(x1,y1),B(x2,y2),
x1+x2=3p,x1x2=
.
则
=(x1-
,y1),
=(x2-
,y2).
∴
•
=(x1-
)(x2-
)+y1y2=
x1x2-
(x1+x2)+
p2=0;
(2)设直线l:x=ky-
,与抛物线联立得y2-2pky+p2=0.
∴y1+y2=2p,y1y2=p2.
则k1+k2=
+
=
+
=
=
=0.
| ||
| 2 |
| p |
| 2 |
联立
|
| p2 |
| 4 |
设A(x1,y1),B(x2,y2),
x1+x2=3p,x1x2=
| p2 |
| 4 |
则
| FA |
| p |
| 2 |
| FB |
| p |
| 2 |
∴
| FA |
| FB |
| p |
| 2 |
| p |
| 2 |
| 3 |
| 2 |
| p |
| 4 |
| 3 |
| 8 |
(2)设直线l:x=ky-
| p |
| 2 |
∴y1+y2=2p,y1y2=p2.
则k1+k2=
| y1 | ||
x1-
|
| y2 | ||
x2-
|
| y1 |
| ky1-p |
| y2 |
| ky2-p |
| 2ky1y2-p(y1+y2) |
| (ky1-p)(ky2-p) |
| 2kp2-p•2pk |
| (ky1-p)(ky2-p) |
点评:本题考查了抛物线的简单几何性质,考查了直线与圆锥曲线的关系,涉及直线与圆锥曲线的关系问题,常利用一元二次方程的根与系数关系,采用设而不求的方法解决,此题属中高档题.

练习册系列答案
相关题目
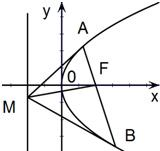 设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A,B两点,且A,B两点坐标分别为(x1,y1)、(x2,y2),y1>0,y2<0,M是抛物线的准线上的一点,O是坐标原点.若直线MA,MF,MB的斜率分别记为:KMA=a,KMF=b,KMB=c,(如图)
设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A,B两点,且A,B两点坐标分别为(x1,y1)、(x2,y2),y1>0,y2<0,M是抛物线的准线上的一点,O是坐标原点.若直线MA,MF,MB的斜率分别记为:KMA=a,KMF=b,KMB=c,(如图)