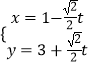题目内容
【题目】已知椭圆E: ![]() (a>b>0)的上顶点为P(0,1),过E的焦点且垂直长轴的弦长为1.若有一菱形ABCD的顶点A、C在椭圆E上,该菱形对角线BD所在直线的斜率为﹣1.
(a>b>0)的上顶点为P(0,1),过E的焦点且垂直长轴的弦长为1.若有一菱形ABCD的顶点A、C在椭圆E上,该菱形对角线BD所在直线的斜率为﹣1.
(1)求椭圆E的方程;
(2)当直线BD过点(1,0)时,求直线AC的方程;
(3)当∠ABC= ![]() 时,求菱形ABCD面积的最大值.
时,求菱形ABCD面积的最大值.
【答案】
(1)解:依题意,b=1,
解 ![]() ,得|y|=
,得|y|= ![]() ,
,
所以 ![]() ,a=2,
,a=2,
椭圆E的方程为 ![]()
(2)解:直线BD:y=﹣1×(x﹣1)=﹣x+1,
设AC:y=x+b,
由方程组 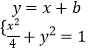 得
得 ![]() ,
,
当 ![]() 时,
时,
A(x1,y1),C(x2,y2)的中点坐标为 ![]() =﹣
=﹣ ![]() ,
, ![]() ,
,
ABCD是菱形,所以AC的中点在BD上,所以 ![]()
解得 ![]() ,满足△=5﹣b2>0,所以AC的方程为y=x﹣
,满足△=5﹣b2>0,所以AC的方程为y=x﹣ ![]()
(3)解:因为四边形ABCD为菱形,且 ![]() ,所以AB=AC=BC,所以菱形ABCD的面积
,所以AB=AC=BC,所以菱形ABCD的面积 ![]() ,
,
由(2)可得AC2=(x2﹣x1)2+(y2﹣y2)2=2,
AC2=(x2﹣x1)2+(y2﹣y1)2=2(x2﹣x1)2=2(x2+x1)2﹣8x1x2=2× ![]() =
= ![]() ,
,
因为 ![]() ,所以当且仅当b=0时,菱形ABCD的面积取得最大值,最大值为
,所以当且仅当b=0时,菱形ABCD的面积取得最大值,最大值为 ![]()
【解析】(1)依题意,b=1,解 ![]() ,得|y|=
,得|y|= ![]() ,所以
,所以 ![]() ,由此能求出椭圆E的方程.(2)直线BD:y=﹣1×(x﹣1)=﹣x+1,设AC:y=x+b,由方程组
,由此能求出椭圆E的方程.(2)直线BD:y=﹣1×(x﹣1)=﹣x+1,设AC:y=x+b,由方程组 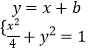 得
得 ![]() ,再由根的判别式、中点坐标公式和菱形的性质能推导出AC的方程.(3)因为四边形ABCD为菱形,且
,再由根的判别式、中点坐标公式和菱形的性质能推导出AC的方程.(3)因为四边形ABCD为菱形,且 ![]() ,所以AB=AC=BC,所以菱形ABCD的面积
,所以AB=AC=BC,所以菱形ABCD的面积 ![]() ,由AC2=(x2﹣x1)2+(y2﹣y1)2=2(x2﹣x1)2=2(x2+x1)2﹣8x1x2=
,由AC2=(x2﹣x1)2+(y2﹣y1)2=2(x2﹣x1)2=2(x2+x1)2﹣8x1x2= ![]() ,能推导出当且仅当b=0时,菱形ABCD的面积取得最大值.
,能推导出当且仅当b=0时,菱形ABCD的面积取得最大值.
【考点精析】根据题目的已知条件,利用一般式方程和椭圆的标准方程的相关知识可以得到问题的答案,需要掌握直线的一般式方程:关于![]() 的二元一次方程
的二元一次方程![]() (A,B不同时为0);椭圆标准方程焦点在x轴:
(A,B不同时为0);椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.