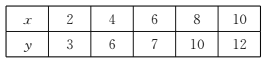
题目内容
【题目】设集合A={x|x2+4x=0,x∈R},B={x|x2+2(a+1)x+a2﹣1=0,x∈R},
(1)若A∩B=A∪B,求实数a的值;
(2)若A∩B=B,求实数a的取值范围.
【答案】
(1)解:A={x|x2+4x=0,x∈R}={0,﹣4}
若A∩B=A∪B,则A=B,
则有a+1=2且a2﹣1=0,
解可得a=1
(2)解:若A∩B=B,则BA
∴B=或{0}或{﹣4}或{0,﹣4};
①当B=时,△=[2(a+1)]2﹣4(a2﹣1)<0a<﹣1
②当B={0}时, ![]() a=﹣1
a=﹣1
③当B={﹣4}时, ![]() a不存在
a不存在
④当B={0,﹣4}时, ![]() a=1
a=1
∴a的取值范围为(﹣∞,﹣1]∪{1}
【解析】(1)解x2+4x=0可得集合A,又由A∩B=A∪B可得A=B,即方程x2+2(a+1)x+a2﹣1=0的两根为0、﹣4,由根与系数的关系可得关于a的方程,解可得答案;(2)根据题意,由A∩B=B可得BA,进而可得B=或{0}或{﹣4}或{0,﹣4},分别求出a的值,综合可得答案.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目