题目内容
设{an}是首项为a,公差为d的等差数列(d≠0),Sn是其前n项和.记bn= ,n∈N*,其中c为实数.
,n∈N*,其中c为实数.
(1)若c=0,且b1,b2,b4成等比数列,证明:Snk=n2Sk(k,n∈N*);
(2)若{bn}是等差数列,证明:c=0.
 ,n∈N*,其中c为实数.
,n∈N*,其中c为实数.(1)若c=0,且b1,b2,b4成等比数列,证明:Snk=n2Sk(k,n∈N*);
(2)若{bn}是等差数列,证明:c=0.
(1)见解析(2)见解析
∵{an}是首项为a,公差为d的等差数列(d≠0),Sn是其前n项和,
∴Sn=na+ d.
d.
(1)∵c=0,∴bn=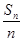 =a+
=a+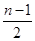 d.
d.
∵b1,b2,b4成等比数列,∴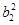 =b1b4,
=b1b4,
∴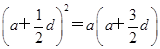 ,∴
,∴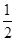 ad-
ad-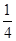 d2=0,∴
d2=0,∴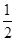 d
d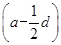 =0.
=0.
∵d≠0,∴a=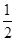 d,∴d=2a,∴Sn=na+
d,∴d=2a,∴Sn=na+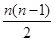 d=na+
d=na+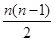 2a=n2a,
2a=n2a,
∴左边=Snk=(nk)2a=n2k2a,右边=n2Sk=n2k2a,
∴左边=右边,∴原式成立.
(2)∵{bn}是等差数列,
∴设公差为d1,
∴bn=b1+(n-1)d1
代入bn= ,得b1+(n-1)d1=
,得b1+(n-1)d1= ,
,
∴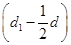 n3+
n3+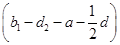 n2+cd1n=c(d1-b1)对n∈N*恒成立,
n2+cd1n=c(d1-b1)对n∈N*恒成立,
∴ ∴d1=
∴d1=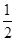 d.∵d≠0,∴d1≠0.
d.∵d≠0,∴d1≠0.
∴Sn=na+
 d.
d.(1)∵c=0,∴bn=
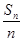 =a+
=a+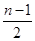 d.
d.∵b1,b2,b4成等比数列,∴
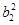 =b1b4,
=b1b4,∴
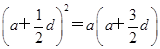 ,∴
,∴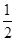 ad-
ad-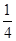 d2=0,∴
d2=0,∴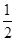 d
d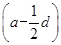 =0.
=0.∵d≠0,∴a=
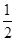 d,∴d=2a,∴Sn=na+
d,∴d=2a,∴Sn=na+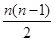 d=na+
d=na+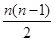 2a=n2a,
2a=n2a,∴左边=Snk=(nk)2a=n2k2a,右边=n2Sk=n2k2a,
∴左边=右边,∴原式成立.
(2)∵{bn}是等差数列,
∴设公差为d1,
∴bn=b1+(n-1)d1
代入bn=
 ,得b1+(n-1)d1=
,得b1+(n-1)d1= ,
,∴
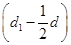 n3+
n3+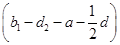 n2+cd1n=c(d1-b1)对n∈N*恒成立,
n2+cd1n=c(d1-b1)对n∈N*恒成立,∴
 ∴d1=
∴d1=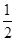 d.∵d≠0,∴d1≠0.
d.∵d≠0,∴d1≠0.
练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
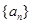 中共有奇数项,且此数列中的奇数项之和为
中共有奇数项,且此数列中的奇数项之和为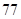 ,偶数项之和为
,偶数项之和为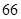 ,
,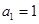 ,则该数列的中间项等于_________.
,则该数列的中间项等于_________.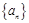 的前
的前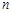 项和为
项和为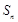 ,若
,若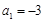 ,
,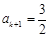 ,
,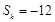 ,则正整数
,则正整数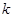 = .
= .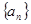 的前
的前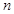 项和为
项和为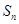 ,若
,若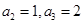 ,则
,则
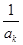 ,
,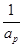 ,
,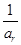 成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由.
成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由.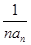 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.