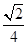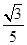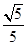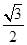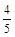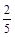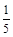题目内容
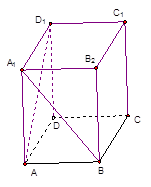
已知长方体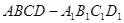 中,
中, ,E、F分别为
,E、F分别为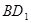 和AD的中点,则异面直线
和AD的中点,则异面直线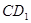 、EF所成的角为( )
、EF所成的角为( )
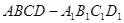 中,
中, ,E、F分别为
,E、F分别为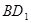 和AD的中点,则异面直线
和AD的中点,则异面直线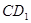 、EF所成的角为( )
、EF所成的角为( )A.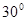 | B. | C.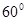 | D.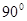 |
D
取CD的中点G,利用三角形中位线的性质可得∠GEF或其补角即为异面直线CD1与EF所成的角.再利用勾股定理可得△EFG为等腰直角三角形,得到∠GEF=45°,从而求得异面直线CD1与EF所成的角为900,选D

练习册系列答案
相关题目
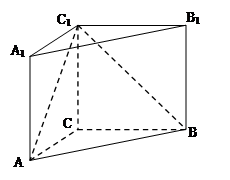
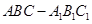 中,
中,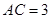 ,
,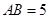 ,
, .
.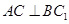 ;
;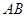 线段上存在一点
线段上存在一点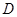 ,使得
,使得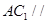 平面
平面 ?
?
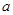 ,
,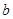 ,
,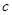 是三条直线,
是三条直线,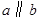 ,且
,且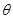 ,那么
,那么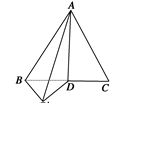
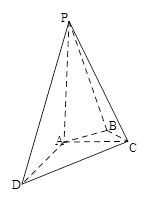
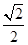 ,E为侧棱PC的中点,则PA与BE所成的角为( )
,E为侧棱PC的中点,则PA与BE所成的角为( )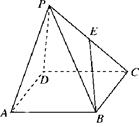
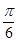
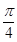
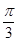

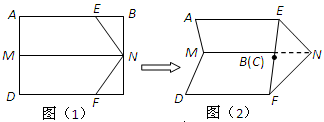
 (B)
(B)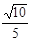 (C)
(C)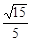 (D)
(D)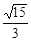
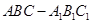 的侧棱长与底面边长都相等.点
的侧棱长与底面边长都相等.点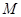 是线段
是线段 的中点,则直线
的中点,则直线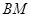 与侧面
与侧面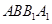 所成角的正切值等于 ( )
所成角的正切值等于 ( )