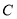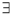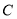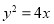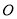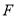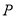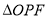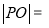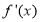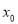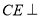题目内容
已知椭圆 :
: 经过点
经过点 ,
, .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设椭圆 的左、右焦点分别为
的左、右焦点分别为 ,过点
,过点 的直线交椭圆
的直线交椭圆 于
于 两点,求
两点,求 面积的最大值.
面积的最大值.
(Ⅰ)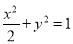 ;(Ⅱ)
;(Ⅱ)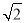
【解析】
试题分析:(Ⅰ)将两点坐标代入椭圆方程组成方程组,即可求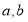 的值。(Ⅱ)由椭圆方程可知
的值。(Ⅱ)由椭圆方程可知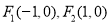 。可分直线斜率存在和不存在两种情况讨论,为了省去讨论也可直接设直线
。可分直线斜率存在和不存在两种情况讨论,为了省去讨论也可直接设直线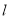 方程为
方程为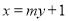 。与椭圆联立方程,消去
。与椭圆联立方程,消去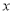 整理可得关于
整理可得关于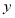 的一元二次方程,因为有两个交点即方程有两根,所以判别式应大于0。然后用韦达定理得根与系数的关系。求
的一元二次方程,因为有两个交点即方程有两根,所以判别式应大于0。然后用韦达定理得根与系数的关系。求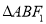 面积时可先求截得的弦长,再求点
面积时可先求截得的弦长,再求点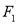 到直线的距离,从而可求面积(此种方法计算量过大)。另一方法求
到直线的距离,从而可求面积(此种方法计算量过大)。另一方法求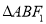 面积:可用转化思想将
面积:可用转化思想将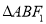 分解成两个小三角形,即
分解成两个小三角形,即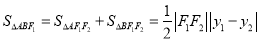 。因为
。因为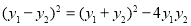 ,可转化为二次函数求最值问题。
,可转化为二次函数求最值问题。
试题解析:【解析】
(Ⅰ)由题意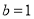 ,椭圆
,椭圆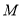 的方程为
的方程为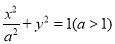 . 1分
. 1分
将点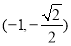 代入椭圆方程,得
代入椭圆方程,得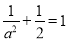 ,解得
,解得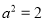 .
.
所以 椭圆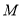 的方程为
的方程为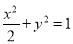 . 3分
. 3分
(Ⅱ)由题意可设直线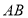 的方程为:
的方程为: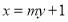 .
.
由 得
得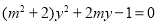 .
.
显然 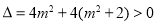 .
.
设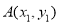 ,
,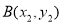 ,则
,则 7分
7分
因为 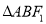 的面积
的面积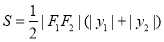 ,其中
,其中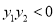 .
.
所以 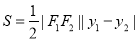 .
.
又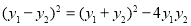
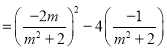
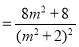 ,
,
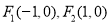 . 9分
. 9分

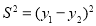
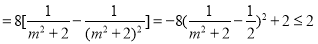 .
.
当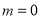 时,上式中等号成立.
时,上式中等号成立.
即当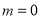 时,
时,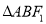 的面积取到最大值
的面积取到最大值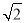 . 11分
. 11分
考点:1椭圆方程;2直线与椭圆的位置关系;3三角形面积;4最值问题。

练习册系列答案
相关题目