Question

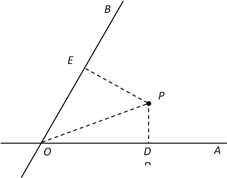
【题目】如图，、是两条公路（近似看成两条直线），，在内有一纪念塔（大小忽略不计），已知到直线、的距离分别为、，=6千米，=12千米．现经过纪念塔修建一条直线型小路，与两条公路、分别交于点、．

（1）求纪念塔到两条公路交点处的距离；

（2）若纪念塔为小路的中点，求小路的长．

Answer 1

【答案】（1）到点处的距离为千米；（2）小路的长为24千米.

【解析】试题分析：

(1)建立平面直角坐标系，结合点到直线距离公式可得到点处的距离为千米；

(2)利用两点之间的距离公式有小路的长为24千米.

试题解析：

解法一：（1）以为原点，所在直线为轴，建立直角坐标系，

则直线的方程为，

又到直线的距离=6千米，设，

所以，解得或（舍负），所以. 7分

（2）因为小路的中点，点在轴上，即，所以，

又点在上，所以，所以，

由（1）知，所以，

.

答：（1）到点处的距离为千米；（2）小路的长为24千米.

解法二：（1）设，则，

因到直线、的距离分别为、，=6千米，=12千米，

所以，

所以，化简得，

又，所以，.

（2）设，则，

因为小路的中点，即，

所以，即，

解得，所以.

答：（1）到点处的距离为千米；（2）小路的长为24千米.