题目内容
若直线y=x-m与曲线y=
有两个不同的交点,则实数m的取值范围是______.
| 1-x2 |
∵y=
表示的曲线为圆心在原点,半径是1的圆在x轴以及x轴上方的部分.
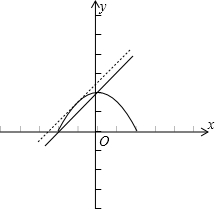
作出曲线y=
的图象,在同一坐标系中,再作出直线y=x-m,平移过程中,直线先与圆相切,再与圆有两个交点,
直线与曲线相切时,可得,
=1
∴m=-
当直线y=x-m经过点(-1,0)时,m=-1,直线y=x+1,而该直线也经过(0,1),即直线y=x+1与半圆有2个交点
故答案为:(-
,-1)
| 1-x2 |
作出曲线y=
| 1-x2 |
直线与曲线相切时,可得,
| |-m| | ||
|
∴m=-
| 2 |
当直线y=x-m经过点(-1,0)时,m=-1,直线y=x+1,而该直线也经过(0,1),即直线y=x+1与半圆有2个交点
故答案为:(-
| 2 |


练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
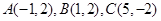 ,若分别以
,若分别以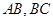 为弦作两外切的圆
为弦作两外切的圆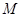 和圆
和圆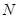 ,且两圆半径相等,则圆的半径为 .
,且两圆半径相等,则圆的半径为 .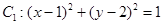 ,圆
,圆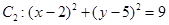 ,则这两圆公切线的条数
,则这两圆公切线的条数