题目内容
已知函数f(x)=eax-x,其中a≠0.
(1)若对一切x∈R,f(x)≥1恒成立,求a的取值集合.
(2)在函数f(x)的图象上取定两点A(x1,f(x1)),B(x2,f(x2)(x1<x2),记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使f′(x0)>k成立?若存在,求x0的取值范围;若不存在,请说明理由.
(1)若对一切x∈R,f(x)≥1恒成立,求a的取值集合.
(2)在函数f(x)的图象上取定两点A(x1,f(x1)),B(x2,f(x2)(x1<x2),记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使f′(x0)>k成立?若存在,求x0的取值范围;若不存在,请说明理由.
(1)若a<0,则对一切x>0,函数f(x)=eax-x<1,这与题设矛盾,
∵a≠0,∴a>0
∵f′(x)=aeax-1,令f′(x)=0,可得x=
ln
令f′(x)<0,可得x<
ln
,函数单调减;令f′(x)>0,可得x>
ln
,函数单调增,
∴x=
ln
时,f(x)取最小值f(
ln
)=
-
ln
∴对一切x∈R,f(x)≥1恒成立,则
-
ln
≥1①
令g(t)=t-tlnt,则g′(t)=-lnt
当0<t<1时,g′(t)>0,g(t)单调递增;当t>1时,g′(t)<0,g(t)单调递减
∴t=1时,g(t)取最大值g(1)=1
∴当且仅当
=1,即a=1时,①成立
综上所述,a的取值集合为{1};
(2)由题意知,k=
-1
令φ(x)=f′(x)-k=aeax-
,则φ(x1)=-
[ea(x2-x1)-a(x2-x1)-1]
φ(x2)=
[ea(x1-x2)-a(x1-x2)-1]
令F(t)=et-t-1,则F′(t)=et-1
当t<0时,F′(t)<0,函数单调减;当t>0时,F′(t)>0,函数单调增;
∴t≠0时,F(t)>F(0)=0,即et-t-1>0
∴ea(x2-x1)-a(x2-x1)-1>0,ea(x1-x2)-a(x1-x2)-1>0
∵
>0,
>0
∴φ(x1)<0,φ(x2)>0
∴存在c∈(x1,x2),φ(c)=0
∵φ′(x)单调递增,故这样的c是唯一的,且c=
ln
当且仅当x∈(
ln
,x2)时,f′(x)>k
综上所述,存在x0∈(x1,x2),使f′(x0)>k成立,且x0的取值范围为(
ln
,x2)
∵a≠0,∴a>0
∵f′(x)=aeax-1,令f′(x)=0,可得x=
| 1 |
| a |
| 1 |
| a |
令f′(x)<0,可得x<
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
∴x=
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
∴对一切x∈R,f(x)≥1恒成立,则
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
令g(t)=t-tlnt,则g′(t)=-lnt
当0<t<1时,g′(t)>0,g(t)单调递增;当t>1时,g′(t)<0,g(t)单调递减
∴t=1时,g(t)取最大值g(1)=1
∴当且仅当
| 1 |
| a |
综上所述,a的取值集合为{1};
(2)由题意知,k=
| eax2-eax1 |
| x2-x1 |
令φ(x)=f′(x)-k=aeax-
| eax2-eax1 |
| x2-x1 |
| eax1 |
| x2-x1 |
φ(x2)=
| eax2 |
| x2-x1 |
令F(t)=et-t-1,则F′(t)=et-1
当t<0时,F′(t)<0,函数单调减;当t>0时,F′(t)>0,函数单调增;
∴t≠0时,F(t)>F(0)=0,即et-t-1>0
∴ea(x2-x1)-a(x2-x1)-1>0,ea(x1-x2)-a(x1-x2)-1>0
∵
| eax1 |
| x2-x1 |
| eax2 |
| x2-x1 |
∴φ(x1)<0,φ(x2)>0
∴存在c∈(x1,x2),φ(c)=0
∵φ′(x)单调递增,故这样的c是唯一的,且c=
| 1 |
| a |
| eax2-eax1 |
| a(x2-x1) |
当且仅当x∈(
| 1 |
| a |
| eax2-eax1 |
| a(x2-x1) |
综上所述,存在x0∈(x1,x2),使f′(x0)>k成立,且x0的取值范围为(
| 1 |
| a |
| eax2-eax1 |
| a(x2-x1) |

练习册系列答案
相关题目
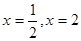 ,曲线
,曲线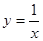 及
及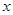 轴所围图形的面积为
轴所围图形的面积为 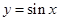 ,x∈[0,2π]与直线y=0围成的两个封闭区域面积之和为()
,x∈[0,2π]与直线y=0围成的两个封闭区域面积之和为()