题目内容
设函数f(x)=1-x2+ln(x+1)
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若不等式f(x)>
-x2(k∈N*)在(0,+∞)上恒成立,求k的最大值.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若不等式f(x)>
| kx |
| x+1 |
(Ⅰ)函数f(x)的定义域为(-1,+∞),
函数f(x)的导数f'(x)=-2x+
,
令f'(x)>0则
>2x,
解得
<x<
,
令f'(x)<0则
<2x,
解得x>
或x<
,
∵x>-1,
∴f(x)的单调增区间为(-1,
),
单调减区间为(
,+∞);
(Ⅱ)不等式f(x)>
-x2
即1-x2+ln(x+1)>
-x2,即1+ln(x+1)>
,
即(x+1)[1+ln(x+1)]>kx(k∈N*)在(0,+∞)上恒成立,
令g(x)=(x+1))[1+ln(x+1)]-kx,则
g'(x)=2+ln(x+1)-k,
∵x>0,∴2+ln(x+1)>2,
若k≤2,则g'(x)>0,即g(x)在(0,+∞)上递增,
∴g(x)>g(0)即g(x)>1>0,
∴(x+1)[1+ln(x+1)]>kx(k∈N*)在(0,+∞)上恒成立;
若k>2则g(x)不为单调函数.
故k的最大值为2.
函数f(x)的导数f'(x)=-2x+
| 1 |
| x+1 |
令f'(x)>0则
| 1 |
| x+1 |
解得
-1-
| ||
| 2 |
-1+
| ||
| 2 |
令f'(x)<0则
| 1 |
| x+1 |
解得x>
-1+
| ||
| 2 |
-1-
| ||
| 2 |
∵x>-1,
∴f(x)的单调增区间为(-1,
| ||
| 2 |
单调减区间为(
| ||
| 2 |
(Ⅱ)不等式f(x)>
| kx |
| x+1 |
即1-x2+ln(x+1)>
| kx |
| x+1 |
| kx |
| x+1 |
即(x+1)[1+ln(x+1)]>kx(k∈N*)在(0,+∞)上恒成立,
令g(x)=(x+1))[1+ln(x+1)]-kx,则
g'(x)=2+ln(x+1)-k,
∵x>0,∴2+ln(x+1)>2,
若k≤2,则g'(x)>0,即g(x)在(0,+∞)上递增,
∴g(x)>g(0)即g(x)>1>0,
∴(x+1)[1+ln(x+1)]>kx(k∈N*)在(0,+∞)上恒成立;
若k>2则g(x)不为单调函数.
故k的最大值为2.

练习册系列答案
相关题目
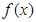 在
在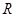 上可导,
上可导,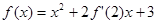 ,则
,则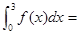 ____________.
____________. (ex+2x)dx等于( )
(ex+2x)dx等于( ) = 。
= 。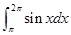 = .
= .