题目内容
已知函数f(x)=x-1-lnx
(Ⅰ)求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)求函数f(x)的极值;
(Ⅲ)对?x∈(0,+∞),f(x)≥bx-2恒成立,求实数b的取值范围.
(Ⅰ)求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)求函数f(x)的极值;
(Ⅲ)对?x∈(0,+∞),f(x)≥bx-2恒成立,求实数b的取值范围.
(Ⅰ)函数的定义域为(0,+∞),f′(x)=1-
,
则f′(2)=
,f(2)=1-ln2,
∴曲线y=f(x)在点(2,f(2))处的切线方程为y-(1-ln2)=
(x-2),
即x-2y-2ln2=0;
(Ⅱ)f′(x)=1-
,
令f′(x)>0,得x>1,
列表:
∴函数y=f(x)的极小值为f(1)=0;
(Ⅲ)依题意对?x∈(0,+∞),f(x)≥bx-2恒成立
等价于x-1-lnx≥bx-2在(0,+∞)上恒成立
可得b≤1+
-
在(0,+∞)上恒成立,
令g(x)=1+
-
,g′(x)=
令g′(x)=0,得x=e2
列表:
∴函数y=g(x)的最小值为g(e2)=1-
,
根据题意,b≤1-
.
| 1 |
| x |
则f′(2)=
| 1 |
| 2 |
∴曲线y=f(x)在点(2,f(2))处的切线方程为y-(1-ln2)=
| 1 |
| 2 |
即x-2y-2ln2=0;
(Ⅱ)f′(x)=1-
| 1 |
| x |
令f′(x)>0,得x>1,
列表:
| x | (0,1) | 1 | (1,+∞) |
| f′(x) | - | 0 | + |
| f(x) | ↘ | 0 | ↗ |
(Ⅲ)依题意对?x∈(0,+∞),f(x)≥bx-2恒成立
等价于x-1-lnx≥bx-2在(0,+∞)上恒成立
可得b≤1+
| 1 |
| x |
| lnx |
| x |
令g(x)=1+
| 1 |
| x |
| lnx |
| x |
| lnx-2 |
| x2 |
令g′(x)=0,得x=e2
列表:
| x | (0,e2) | e2 | (e2,+∞) | ||
| g'(x) | - | 0 | + | ||
| g(x) | ↘ | 1-
| ↗ |
| 1 |
| e2 |
根据题意,b≤1-
| 1 |
| e2 |

练习册系列答案
相关题目
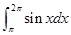 = .
= .