题目内容
统计表明某型号汽车在匀速行驶中每小时的耗油量y(升)关于行驶速度x(千米/小时)的函数为y=
x3-
x+8(0<x<120).
(1)当x=64千米/小时时,要行驶100千米耗油量多少升?
(2)若油箱有22.5升油,则该型号汽车最多行驶多少千米?
| 1 |
| 128000 |
| 3 |
| 80 |
(1)当x=64千米/小时时,要行驶100千米耗油量多少升?
(2)若油箱有22.5升油,则该型号汽车最多行驶多少千米?
(1)当x=64千米/小时时,要行驶100千米需要
=
小时
需要耗油((
×643-
×64+8)×
=11.95(升)
(2)设22.5升油该型号汽车可行驶a千米,由题意得(
x3-
•x+8)×
=22.5
∴a=
设h(x)=
x2+
-
则当h(x)最小时,a取最大值,
由h′(x)=
x2-
=
,
令h'(x)=0⇒x=80当x∈(0,80)时,h'(x)<0,当x∈(80,120)时,h'(x)>0.
故当x∈(0,80)时,函数h(x)为减函数,当x∈(80,120)时,函数h(x)为增函数.
∴当x=80时,h(x)取得最小值,此时a取最大值为a=
=200.
答:若油箱有22.5升油,则该型号汽车最多行驶200千米.
| 100 |
| 64 |
| 25 |
| 16 |
需要耗油((
| 1 |
| 128000 |
| 3 |
| 80 |
| 25 |
| 16 |
(2)设22.5升油该型号汽车可行驶a千米,由题意得(
| 1 |
| 128000 |
| 3 |
| 80 |
| a |
| x |
∴a=
| 22.5 | ||||||
|
设h(x)=
| 1 |
| 128000 |
| 8 |
| x |
| 3 |
| 80 |
由h′(x)=
| 1 |
| 64000 |
| 8 |
| x2 |
| x3-803 |
| 64000x2 |
令h'(x)=0⇒x=80当x∈(0,80)时,h'(x)<0,当x∈(80,120)时,h'(x)>0.
故当x∈(0,80)时,函数h(x)为减函数,当x∈(80,120)时,函数h(x)为增函数.
∴当x=80时,h(x)取得最小值,此时a取最大值为a=
| 22.5 | ||||||
|
答:若油箱有22.5升油,则该型号汽车最多行驶200千米.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目

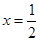 ,
,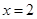 ,曲线
,曲线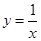 及
及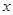 轴所围成的图形的面积是( )
轴所围成的图形的面积是( )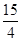
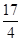
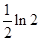
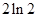
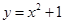 与直线
与直线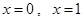 及
及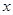 轴所围成的图形的面积是 .
轴所围成的图形的面积是 . = 。
= 。