题目内容
14.已知f(x)=x2+2x+1-sina−b3π(Ⅰ)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求函数f(x)有零点的概率
(Ⅱ)若a是从区间[0,3]中任取的一个数,b是从区间[0,2]中任取的一个数,求函数f(x)有零点的概率.
分析 (Ⅰ)问题等价于sina−b3π≥0,列举可得基本事件共有15个,事件A包含6个基本事件,可得概率;
(Ⅱ)作出图形,由几何概型的概率公式可得.
解答 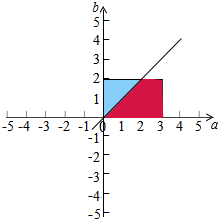 解:(Ⅰ)函数f(x)=x2+2x+1-sina−b3π有零点等价于方程x2+2x+1-sina−b3π=0有实根,
解:(Ⅰ)函数f(x)=x2+2x+1-sina−b3π有零点等价于方程x2+2x+1-sina−b3π=0有实根,
∵x2+2x+1≥0,∴sina−b3π≥0
记事件A为函数f(x)=x2+2x+1-sina−b3π有零点,
总的基本事件共有12个:(0,0),(0,1),(0,2),(1,0),
(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),
(3,2),事件A包含9个基本事件:(0,0),(1,0),(1,1),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2),9个.
∴P(A)=912=34
(Ⅱ)如图,试验的全部结果所构成的区域为(矩形区域)a是从区间[0,3]中任取的一个数,b是从区间[0,2]中任取的一个数,
函数表示事件A,所构成的区域为A={(a,b)|sina−b3π≥0且(a,b)∈Ω}即图中的阴影部分.
∴P(A)=1−12×2×22×3=23.
点评 本题考查古典概型和几何概型,关键是首先明确概率模型,然后根据根式解答;属中档题.

练习册系列答案
相关题目
14.已知a∈(0,π2),且2sin2α-sinα•cosα-3cos2α=0,则sin(α+π4)sin2α+cos2α+1=( )
| A. | √264 | B. | √268 | C. | √134 | D. | √138 |
 如图所示,CD为 Rt△ABC斜边AB边上的中线,CE⊥CD,CE=
如图所示,CD为 Rt△ABC斜边AB边上的中线,CE⊥CD,CE=