题目内容
9.方程2$\sqrt{(x-1)^{2}+(y-1)^{2}}$=|x+y+2|表示的曲线 ( )| A. | 椭圆 | B. | 双曲线 | C. | 线段 | D. | 抛物线 |
分析 观察方程两边分别是到点的距离和到直线的距离,联想椭圆的第二定义.
解答 解:∵2$\sqrt{(x-1)^{2}+(y-1)^{2}}$=|x+y+2|,①
∴$\frac{\sqrt{(x-1)^{2}+(y-1)^{2}}}{\frac{|x+y+2|}{\sqrt{2}}}$=$\frac{\sqrt{2}}{2}$<1.②
即点P(x,y)到定点F(1,1)的距离(x-1)2+(y-1)2与到定直线l:x+y+2=0的距离的比值为e=$\frac{\sqrt{2}}{2}$<1.
点P的轨迹是椭圆.
故选:A.
点评 本题考查曲线与方程,考查椭圆的第二定义,正确转化是关键.

练习册系列答案
相关题目
17.某单位招聘职工分为笔试和面试两个环节,将笔试成绩合格(满分100分,及格60分,精确到个位数)的应聘者进行统计,得到如下的频率分布表:
(I)确定表中a,b,x,y的值(直接写出结果,不必写过程)
(Ⅱ)面试规定,笔试成绩在80分(不含80分)以上者可以进入面试环节,面试时又要分两关,首先面试官依次提出4个问题供选手回答,并规定,答对2道题就终止回答,通过第一关可以进入下一关,如果前三题均没有答对,则不再回答第四题并且不能进入下一关,假定某选手获得面试资格的概率与答对每道题的概率相等.
①求该选手答完3道题而通过第一关的概率;
②记该选手在面试第一关中的答题个数为X,求X的分布列及数学期望.
| 分组 | 频数 | 频率 |
| [60,70] | a | 0.16 |
| (70,80] | 22 | x |
| (80,90] | 14 | 0.28 |
| (90,100] | b | y |
| 合计 | 50 | 1 |
(Ⅱ)面试规定,笔试成绩在80分(不含80分)以上者可以进入面试环节,面试时又要分两关,首先面试官依次提出4个问题供选手回答,并规定,答对2道题就终止回答,通过第一关可以进入下一关,如果前三题均没有答对,则不再回答第四题并且不能进入下一关,假定某选手获得面试资格的概率与答对每道题的概率相等.
①求该选手答完3道题而通过第一关的概率;
②记该选手在面试第一关中的答题个数为X,求X的分布列及数学期望.
4.设$\overrightarrow{a}$,$\overrightarrow{b}$是非零向量,k∈R,则$\overrightarrow{a}$=k$\overrightarrow{b}$是$\overrightarrow{a}$与$\overrightarrow{b}$平行的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分非必要条件 |
19.在直角三角形ABC中,C=90°,B=30°,AB=4,M是AB的中点,将三角形ACM沿CM翻折成直二面角,则三棱锥A-CBM的外接球的表面积为( )
| A. | $\frac{52π}{3}$ | B. | $\frac{18π}{5}$ | C. | $\frac{14π}{3}$ | D. | 12π |
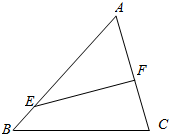 有一块三角形边角地,如图中△ABC,其中AB=8(百米),AC=6(百米),∠A=60°,某市为迎接2500年城庆,欲利用这块地修一个三角形形状的草坪(图中△AEF)供市民休闲,其中点E在边AB上,点F在边AC上,规划部门要求△AEF的面积占△ABC面积的一半,记△AEF的周长为l(百米).
有一块三角形边角地,如图中△ABC,其中AB=8(百米),AC=6(百米),∠A=60°,某市为迎接2500年城庆,欲利用这块地修一个三角形形状的草坪(图中△AEF)供市民休闲,其中点E在边AB上,点F在边AC上,规划部门要求△AEF的面积占△ABC面积的一半,记△AEF的周长为l(百米).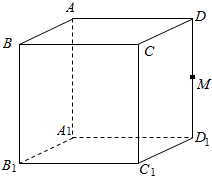 如图,M是正方体ABCD-A1B1C1D1的棱DD1的中点,给出下列命题:
如图,M是正方体ABCD-A1B1C1D1的棱DD1的中点,给出下列命题: