题目内容
设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为( )
| A.y2=4x或y2=8x | B.y2=2x或y2=8x |
| C.y2=4x或y2=16x | D.y2=2x或y2=16x |
∵抛物线C方程为y2=2px(p>0)
∴焦点F坐标为(
,0),可得|OF|=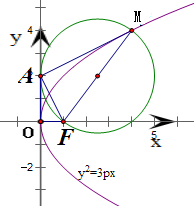
∵以MF为直径的圆过点(0,2),
∴设A(0,2),可得AF⊥AM
Rt△AOF中,|AF|=
=
∴sin∠OAF=
=
∵根据抛物线的定义,得直线AO切以MF为直径的圆于A点,
∴∠OAF=∠AMF,可得Rt△AMF中,sin∠AMF=
=
,
∵|MF|=5,|AF|=
∴
=
,整理得4+
=
,解之可得p=2或p=8
因此,抛物线C的方程为y2=4x或y2=16x
故选:C
∴焦点F坐标为(
| p |
| 2 |

| p |
| 2 |
∵以MF为直径的圆过点(0,2),
∴设A(0,2),可得AF⊥AM
Rt△AOF中,|AF|=
22+(
|
4+
|
∴sin∠OAF=
| |OF| |
| |AF| |
| ||||
|
∵根据抛物线的定义,得直线AO切以MF为直径的圆于A点,
∴∠OAF=∠AMF,可得Rt△AMF中,sin∠AMF=
| |AF| |
| |MF| |
| ||||
|
∵|MF|=5,|AF|=
4+
|
∴
| ||||
| 5 |
| ||||
|
| p2 |
| 4 |
| 5p |
| 2 |
因此,抛物线C的方程为y2=4x或y2=16x
故选:C

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
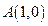 和到定直线
和到定直线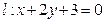 的距离相等的点的轨迹为( )
的距离相等的点的轨迹为( )