题目内容
17．已知点M（1，1），N（4，-3），则与向量$\overrightarrow{MN}$共线的单位向量为（ ）| A． | （$\frac{3}{5}$，-$\frac{4}{5}$） | B． | （-$\frac{3}{5}$，$\frac{4}{5}$） | C． | （$\frac{3}{5}$，-$\frac{4}{5}$）或（-$\frac{3}{5}$，$\frac{4}{5}$） | D． | （$\frac{4}{5}$，-$\frac{3}{5}$）或（-$\frac{4}{5}$，$\frac{3}{5}$） |
分析 由题意可得$\overrightarrow{MN}$=（3，-4），可得|$\overrightarrow{MN}$|=5，单位化即可．
解答 解：∵M（1，1），N（4，-3），
∴$\overrightarrow{MN}$=（4，-3）-（1，1）=（3，-4），
∴|$\overrightarrow{MN}$|=$\sqrt{{3}^{2}+（-4）^{2}}$=5，
∴与向量$\overrightarrow{MN}$共线的单位向量为$\frac{1}{5}$（3，-4）=（$\frac{3}{5}$，-$\frac{4}{5}$），
或-$\frac{1}{5}$（3，-4）=（-$\frac{3}{5}$，$\frac{4}{5}$），
故选：C．
点评 本题考查平行向量和共线向量，涉及模长公式，属基础题．
练习册系列答案
相关题目
17．
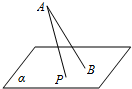如图，斜线段AB与平面α所成的角为60°，B为斜足，平面α上的动点P满足∠PAB=30°，则点P的轨迹是（ ）
如图，斜线段AB与平面α所成的角为60°，B为斜足，平面α上的动点P满足∠PAB=30°，则点P的轨迹是（ ）| A． | 直线 | B． | 抛物线 | C． | 椭圆 | D． | 双曲线的一支 |
8．
如图，圆锥的底面直径AB=2，母线长VA=3，点C在母线长VB上，且VC=1，有一只蚂蚁沿圆锥的侧面从点A到点C，则这只蚂蚁爬行的最短距离是（ ）
如图，圆锥的底面直径AB=2，母线长VA=3，点C在母线长VB上，且VC=1，有一只蚂蚁沿圆锥的侧面从点A到点C，则这只蚂蚁爬行的最短距离是（ ）| A． | $\sqrt{13}$ | B． | $\sqrt{7}$ | C． | $\frac{4\sqrt{3}}{3}$ | D． | $\frac{3\sqrt{3}}{2}$ |
12．A、B是半径为2的圆O上的两点，M是弦AB上的动点，若△AOB为直角三角形，则$\overrightarrow{OM}$•$\overrightarrow{AM}$的最小值为（ ）
| A． | -1 | B． | -$\frac{1}{2}$ | C． | 0 | D． | 2 |
9．已知在△ABC中，a、b、c分别是三个内角∠A、∠B、∠C的对边，且$\frac{sinA-sinC}{sinB}$=$\frac{sinA-sinB}{sinA+sinC}$，则∠C=（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{5π}{6}$ | D． | $\frac{2π}{3}$ |