题目内容
14.已知函数f(x)=alnx+bx在x=1处的切线与直线x-y+1=0平行,函数f(x)在[1,e]上是单调函数且最小值为0.(1)求实数a,b;
(2)对一切x∈(0,+∞),xf(x)≤x2-cx+12恒成立,求实数c的取值范围.
分析 (1)求出f(x)的导数,求得切线的斜率,由两直线平行的条件,可得a+b=1,讨论f(x)在[1,e]的单调性,可得最小值,解方程即可得到a,b,注意检验;
(2)运用参数分离,可得c≤x+$\frac{12}{x}$-lnx在(0,+∞)恒成立.令g(x)=x+$\frac{12}{x}$-lnx,x>0,求得导数和单调区间,即可得到最小值,即可得到c的范围.
解答 解:(1)函数f(x)=alnx+bx的导数为f′(x)=b+$\frac{a}{x}$,
即有在x=1处的切线斜率为a+b,
由题意可得a+b=1,
若函数f(x)在[1,e]上是单调递增,则f(1)=0,
即有b=0,a=1;
若函数f(x)在[1,e]上是单调递减,则f(e)=0,
即有a+be=0,解得a=$\frac{-e}{1-e}$,b=$\frac{1}{1-e}$,
即有f′(x)=$\frac{1}{1-e}$-$\frac{ex}{1-e}$,在[1,e]上f′(x)>0,
即有f(x)在[1,e]上递增,不成立.
则有a=1,b=0;
(2)f(x)=lnx,
对一切x∈(0,+∞),xf(x)≤x2-cx+12恒成立,
即有c≤x+$\frac{12}{x}$-lnx在(0,+∞)恒成立.
令g(x)=x+$\frac{12}{x}$-lnx,x>0,
g′(x)=1-$\frac{12}{{x}^{2}}$-$\frac{1}{x}$=$\frac{(x-4)(x+3)}{{x}^{2}}$,
当x>4时,g′(x)>0,g(x)递增;
当0<x<4时,g′(x)<0,g(x)递减.
即有g(x)在x=4处取得极小值,也为最小值,且为7-2ln2,
则有c≤7-2ln2.
则c的取值范围是(-∞,7-4ln2].
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,主要考查导数的几何意义和二次不等式的解法,运用参数分离和函数的单调性是解题的关键.

| A. | 1997 | B. | 1999 | C. | 2012 | D. | 2016 |
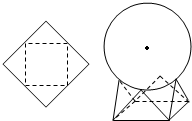 如图,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将表面积为4π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋中心(球心)与蛋巢底面的距离为$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$.
如图,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将表面积为4π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋中心(球心)与蛋巢底面的距离为$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$.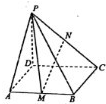 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PD⊥底面ABCD,M,N分别为AB,PC的中点,PD=AD=2,AB=4.则点A到平面PMN的距离为$\frac{\sqrt{6}}{3}$.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PD⊥底面ABCD,M,N分别为AB,PC的中点,PD=AD=2,AB=4.则点A到平面PMN的距离为$\frac{\sqrt{6}}{3}$.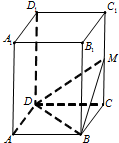 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,点M为CC1的中点,则点D1到平面BDM的距离为$\frac{{2\sqrt{3}}}{3}$.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,点M为CC1的中点,则点D1到平面BDM的距离为$\frac{{2\sqrt{3}}}{3}$.