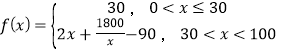Question

【题目】已知点，，点为曲线上任意一点且满足

（1）求曲线的方程；

（2）设曲线与 轴交于两点，点是曲线上异于的任意一点，直线分别交直线：于点，试问轴上是否存在一个定点，使得？若存在，求出点的坐标；若不存在，请说明理由.

Answer 1

【答案】（1）；（2）存在点使得成立.

【解析】

（1）设P（x，y），由|PA|=2|PB|，得=2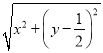，由此能求出曲线的方程．

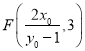（2）由题意得M(0，1)，N(0，-1)，设点R(x0，y0)，（x0≠0），由点R在曲线上，得=1，直线RM的方程，从而直线RM与直线y=3的交点为，直线RN的方程为，从而直线RN与直线y=3的交点为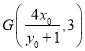，假设存在点S(0，m)，使得成立，则，由此能求出存在点S，使得成立，且S点的坐标为.

（1）设，由，

得：，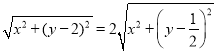

整理得.

所以曲线的方程为.

（2）由题意得，，.

设点，由点在曲线上，

所以.

直线的方程为，

所以直线与直线的交点为.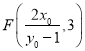

直线的方程为

所以直线与直线的交点为.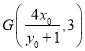

假设存在点，使得成立，

则，.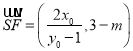

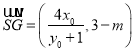即，

整理得.

因为，

所以，

解得.

所以存在点使得成立，且点的坐标为.