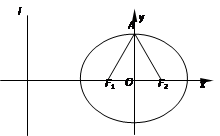题目内容
(本小题满分14分)设椭圆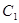 与抛物线
与抛物线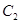 的焦点均在
的焦点均在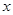 轴上,
轴上,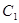 的中心和
的中心和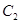 的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
1)求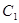 ,
,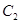 的标准方程, 并分别求出它们的离心率
的标准方程, 并分别求出它们的离心率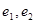 ;
;
2)设直线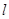 与椭圆
与椭圆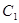 交于不同的两点
交于不同的两点 ,且
,且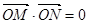 (其中
(其中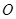 坐标原点),请问是否存在这样的直线
坐标原点),请问是否存在这样的直线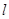 过抛物线
过抛物线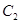 的焦点
的焦点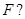 若存在,求出直线
若存在,求出直线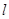 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
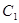 与抛物线
与抛物线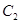 的焦点均在
的焦点均在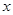 轴上,
轴上,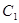 的中心和
的中心和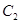 的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中: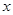 |  |  |  |  | 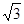 |
 |  |  |  |  |  |
1)求
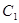 ,
,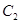 的标准方程, 并分别求出它们的离心率
的标准方程, 并分别求出它们的离心率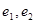 ;
;2)设直线
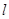 与椭圆
与椭圆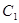 交于不同的两点
交于不同的两点 ,且
,且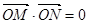 (其中
(其中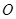 坐标原点),请问是否存在这样的直线
坐标原点),请问是否存在这样的直线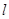 过抛物线
过抛物线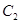 的焦点
的焦点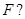 若存在,求出直线
若存在,求出直线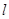 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.(1) ,
, ,
, ,
,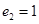 。(2)
。(2) 。
。
 ,
, ,
, ,
,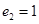 。(2)
。(2) 。
。试题分析:(1)∵焦点在x轴上,且椭圆
 与抛物线
与抛物线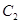 的中心与顶点在原点,又过点
的中心与顶点在原点,又过点 ,
,故点
 在椭圆上,点
在椭圆上,点 在抛物线
在抛物线 上
上 ,
,
∴点
 在
在 上,
上,设

把点
 代入得
代入得 ,
,

由抛物线
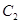 知
知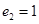
(2)由
 得
得
若l与x轴垂直,则l:x=1
由

设
 不满足
不满足
若存在直线l不与x轴垂直,可设为

设

由








所求的直线为

点评:(1)做第一问的关键是确定哪两个点在椭圆上,哪两个点在抛物线上。(2)在求直线与圆锥曲线相交的有关问题时,通常采用设而不求的方法,在求解过程中一般采取步骤为:设点→联立方程→消元→韦达定理。

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
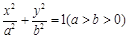 的左焦点为F, 离心率为
的左焦点为F, 离心率为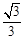 , 过点F且与x轴垂直的直线被椭圆截得的线段长为
, 过点F且与x轴垂直的直线被椭圆截得的线段长为 .
.  , 求k的值.
, 求k的值.  的离心率
的离心率 ,其中一个顶点坐标为
,其中一个顶点坐标为 ,则椭圆的方程为 .
,则椭圆的方程为 .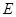 上任意一点
上任意一点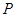 到两个定点
到两个定点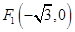 ,
,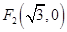 的距离之和为4.
的距离之和为4.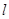 与曲线
与曲线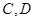 两点,且
两点,且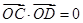 (
(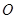 为原点),求直线
为原点),求直线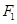 ,
, 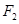 是椭圆
是椭圆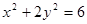 的两个焦点,点
的两个焦点,点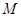 在此椭圆上且
在此椭圆上且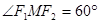 ,则
,则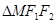 的面积等于( )
的面积等于( )
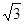

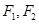 是椭圆
是椭圆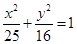 的两个焦点,点M在椭圆上,若△
的两个焦点,点M在椭圆上,若△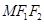 是直角三角形,则△
是直角三角形,则△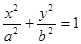 (a>
(a>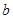 )中,记左焦点为F,右顶点为A,短轴上方的端点为B,若角
)中,记左焦点为F,右顶点为A,短轴上方的端点为B,若角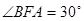 ,则椭圆的离心率为( )
,则椭圆的离心率为( )



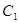 的离心率为
的离心率为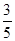 ,焦点在
,焦点在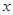 轴上,且长轴长为10,曲线
轴上,且长轴长为10,曲线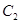 上的点与椭圆
上的点与椭圆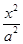 +
+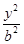 =1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,
=1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,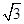 ,
,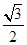 )在椭圆C上,直线l为椭圆C的左准线.
)在椭圆C上,直线l为椭圆C的左准线.