题目内容
已知点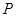 是抛物线
是抛物线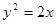 上的动点,点
上的动点,点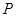 在
在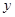 轴上的射影是
轴上的射影是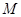 ,
,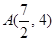 ,则
,则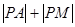 的最小值是 .
的最小值是 .
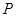 是抛物线
是抛物线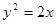 上的动点,点
上的动点,点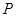 在
在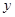 轴上的射影是
轴上的射影是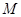 ,
,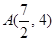 ,则
,则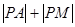 的最小值是 .
的最小值是 .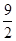
试题分析:易求抛物线
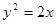 的焦点为
的焦点为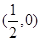 ,而
,而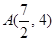 在抛物线的上方,所以
在抛物线的上方,所以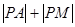 的最小值为点
的最小值为点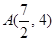 与焦点
与焦点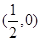 的距离减去
的距离减去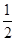 ,而点
,而点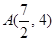 与焦点
与焦点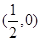 的距离为
的距离为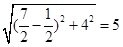 ,所以
,所以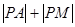 的最小值是
的最小值是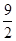 .
.点评:抛物线上的点到焦点的距离等于到准线的距离,这点性质经常用来求最值,解这种题目时还要注意转化思想的应用.

练习册系列答案
相关题目
题目内容
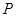 是抛物线
是抛物线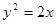 上的动点,点
上的动点,点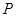 在
在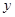 轴上的射影是
轴上的射影是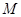 ,
,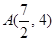 ,则
,则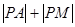 的最小值是 .
的最小值是 .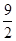
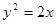 的焦点为
的焦点为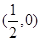 ,而
,而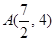 在抛物线的上方,所以
在抛物线的上方,所以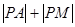 的最小值为点
的最小值为点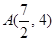 与焦点
与焦点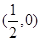 的距离减去
的距离减去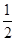 ,而点
,而点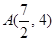 与焦点
与焦点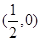 的距离为
的距离为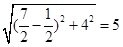 ,所以
,所以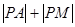 的最小值是
的最小值是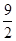 .
.