题目内容
已知椭圆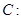
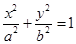 (
(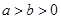 )的一个顶点为
)的一个顶点为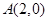 ,离心率为
,离心率为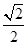 ,直线
,直线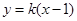 与椭圆
与椭圆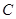 交于不同的两点
交于不同的两点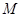 、
、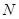 .(1) 求椭圆
.(1) 求椭圆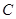 的方程;(2) 当
的方程;(2) 当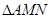 的面积为
的面积为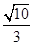 时,求
时,求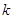 的值.
的值.
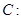
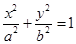 (
(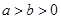 )的一个顶点为
)的一个顶点为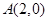 ,离心率为
,离心率为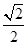 ,直线
,直线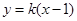 与椭圆
与椭圆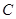 交于不同的两点
交于不同的两点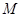 、
、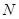 .(1) 求椭圆
.(1) 求椭圆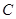 的方程;(2) 当
的方程;(2) 当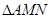 的面积为
的面积为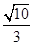 时,求
时,求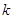 的值.
的值.(1)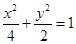 ; (2)
; (2) 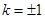 .
.
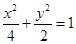 ; (2)
; (2) 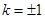 .
.试题分析:(1)易知椭圆的焦点在x轴上,因为椭圆的一个顶点为
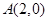 ,所以a=2,又因为离心率为
,所以a=2,又因为离心率为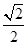 ,所以c=
,所以c=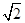 ,所以
,所以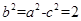 ,所以椭圆的方程为
,所以椭圆的方程为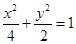 。
。(2)设
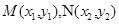 ,联立直线方程和椭圆方程
,联立直线方程和椭圆方程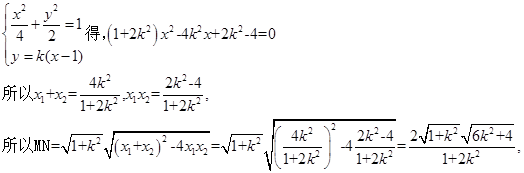
点A到直线
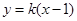 的距离为
的距离为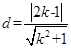 ,
,所以
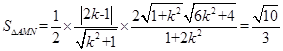 ,解得
,解得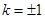 。
。点评:本题主要考查椭圆方程的求法和弦长的运算,解题时要注意椭圆性质的灵活运用和弦长公式的合理运用。在求直线与圆锥曲线相交的弦长时一般采用韦达定理设而不求的方法,在求解过程中一般采取步骤为:设点→联立方程→消元→韦达定理→弦长公式。

练习册系列答案
相关题目
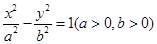 的一条渐近线与直线
的一条渐近线与直线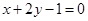 垂直,则曲线的离心率等于 。
垂直,则曲线的离心率等于 。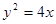 的焦点为F,准线为l,点P为抛物线上一点,且
的焦点为F,准线为l,点P为抛物线上一点,且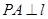 ,垂足为A,若直线AF的斜率为
,垂足为A,若直线AF的斜率为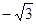 ,则|PF|等于( )
,则|PF|等于( )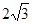
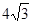
 的两个焦点分别为
的两个焦点分别为 、
、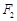 ,则满足△
,则满足△ 的周长为
的周长为 的动点
的动点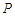 的轨迹方程为 ( )
的轨迹方程为 ( )



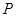 是抛物线
是抛物线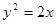 上的动点,点
上的动点,点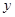 轴上的射影是
轴上的射影是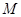 ,
,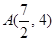 ,则
,则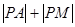 的最小值是 .
的最小值是 .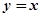 被曲线
被曲线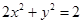 截得的弦长为 ;
截得的弦长为 ; 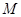 是椭圆
是椭圆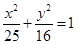 上的一点,
上的一点,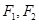 为焦点,且
为焦点,且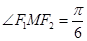 ,则
,则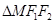 的面积为( )
的面积为( )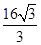
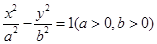 的一个焦点,并与双曲线的实轴垂直,已知抛物线与双曲线的交点为
的一个焦点,并与双曲线的实轴垂直,已知抛物线与双曲线的交点为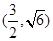 .
.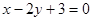 和
和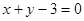 的交点,且满足下列条件的直线
的交点,且满足下列条件的直线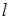 的方程.
的方程.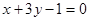 垂直;
垂直;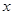 轴,
轴,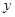 轴上的截距相等.
轴上的截距相等.