题目内容
已知-1<a+b<3,且2<a-b<4,求2a+3b的取值范围.
- <2a+3b<
<2a+3b<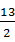
 <2a+3b<
<2a+3b<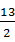
设2a+3b=x(a+b)+y(a-b)=(x+y)a+(x-y)b.则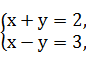 解得
解得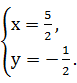
所以2a+3b= (a+b)-
(a+b)- (a-b).
(a-b).
因为-1<a+b<3,2<a-b<4,
所以- <
< (a+b)<
(a+b)<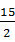 ,-2<-
,-2<- (a-b)<-1.
(a-b)<-1.
所以- -2<2a+3b<
-2<2a+3b<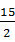 -1,即-
-1,即- <2a+3b<
<2a+3b<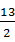 .
.
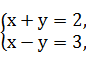 解得
解得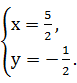
所以2a+3b=
 (a+b)-
(a+b)- (a-b).
(a-b).因为-1<a+b<3,2<a-b<4,
所以-
 <
< (a+b)<
(a+b)<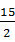 ,-2<-
,-2<- (a-b)<-1.
(a-b)<-1.所以-
 -2<2a+3b<
-2<2a+3b<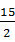 -1,即-
-1,即- <2a+3b<
<2a+3b<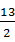 .
.
练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 2
2 .(填不等关系符号)
.(填不等关系符号) ,Q=
,Q= ,则P与Q的大小关系是 ( )
,则P与Q的大小关系是 ( ) >
>
 (n>1,n∈N*)的过程中,用n=k+1时左边的代数式减去n=k时左边的代数式的结果是A,求代数式A.
(n>1,n∈N*)的过程中,用n=k+1时左边的代数式减去n=k时左边的代数式的结果是A,求代数式A. 对任意n∈N*恒成立,求实数a的取值范围.
对任意n∈N*恒成立,求实数a的取值范围.