题目内容
若函数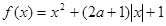 的定义域被分成了四个不同的单调区间,则实数
的定义域被分成了四个不同的单调区间,则实数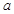 的取值范围是
的取值范围是
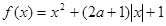 的定义域被分成了四个不同的单调区间,则实数
的定义域被分成了四个不同的单调区间,则实数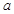 的取值范围是
的取值范围是A.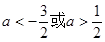 | B.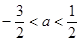 |
C.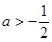 | D.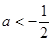 |
D
分析:利用零点分段法将将函数化为分段函数的形式,进而根据二次函数的图象和性质,可得实数a的取值范围.
解:∵函数y=x2+(2a+1)|x|+1
=
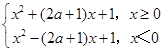
若函数f(x)=x2+(2a+1)|x|+1的定义域被分成了四个不同的单调区间
则函数y=x2+(2a+1)x+1的对称轴x=-
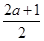 在y轴右侧且函数y=x2-(2a+1)x+1的对称轴x=
在y轴右侧且函数y=x2-(2a+1)x+1的对称轴x=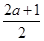 在y轴左侧
在y轴左侧即x=-
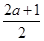 >0且x=
>0且x=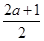 <0
<0解得a<-
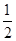
故选D

练习册系列答案
相关题目
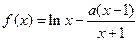 .
.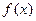 在
在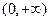 上为单调增函数,求
上为单调增函数,求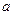 的取值范围;
的取值范围;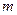 ,
,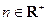 ,且
,且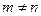 ,求证:
,求证: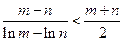 .
. 。
。 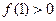 .
.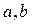 的值
的值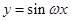 在
在 内是减函数, 则( )
内是减函数, 则( ) 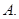

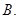
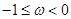




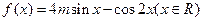 ,若函数
,若函数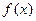 的最大值为3,求实数m的值。
的最大值为3,求实数m的值。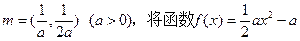 的图象按向量m平移后得到函数
的图象按向量m平移后得到函数 的图象。
的图象。 上的最小值为
上的最小值为 的最大值。
的最大值。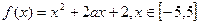 .
.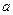 的范围,使
的范围,使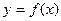 在区间
在区间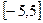 上是单调函数。 (2)求
上是单调函数。 (2)求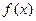 的最小值
的最小值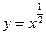
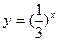
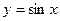

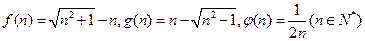 ,用不等号从小到大连结起来为____________.
,用不等号从小到大连结起来为____________.