Question

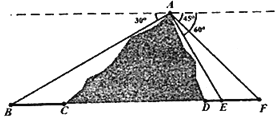
【题目】高铁是我国国家名片之一，高铁的修建凝聚着中国人的智慧与汗水.如图所示，B、E、F为山脚两侧共线的三点，在山顶A处测得这三点的俯角分别为、、，计划沿直线BF开通穿山隧道，现已测得BC、DE、EF三段线段的长度分别为3、1、2.

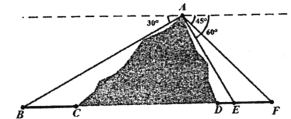
（1）求出线段AE的长度；

（2）求出隧道CD的长度.

Answer 1

【答案】（1）

（2）

【解析】

（1）由已知在△AEF中，由正弦定理即可解得AE的值；（2）由已知可得∠BAE＝90°，在Rt△ABE中，可求BE的值，进而可求CD＝BE﹣BC﹣DE的值．

（1）由已知可得EF＝2，∠F＝45°，∠EAF＝60°－45°＝15°，

在△AEF中，由正弦定理得：，

即，

解得；

（2）由已知可得∠BAE＝180°﹣30°﹣60°＝90°，

在Rt△ABE中，，

所以隧道长度．